
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论:①BE=2AE;②△DFP~△BPH;③![]() ;④DP2=PHPC;其中正确的是( )
;④DP2=PHPC;其中正确的是( )
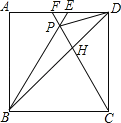
A. ①②③④B. ①③④C. ②③D. ①②④
【答案】D
【解析】
由正方形的性质和相似三角形的判定与性质,即可得出结论.
∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
∴BE=2AE;故①正确;
∵PC=CD,∠PCD=30°,
∴∠PDC=75°,
∴∠FDP=15°,
∵∠DBA=45°,
∴∠PBD=15°,
∴∠FDP=∠PBD,
∵∠DFP=∠BPC=60°,
∴△DFP∽△BPH;故②正确;
∵∠DCF=90°﹣60°=30°,
∴tan∠DCF=![]() ,
,
∵△DFP∽△BPH,
∴![]() ,
,
∵BP=CP=CD,
∴![]() ;故③错误;
;故③错误;
∵∠PDH=∠PCD=30°,∠DPH=∠DPC,
∴△DPH∽△CPD,
∴![]() ,
,
∴DP2=PHPC,故④正确;
故选D.


科目:初中数学 来源: 题型:
【题目】如图,线段 AB 经过⊙O 的圆心, AC , BD 分别与⊙O 相切于点 C ,D .若 AC =BD = 4 ,∠A=45°,则弧CD的长度为( )
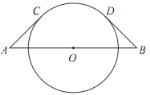
A.πB.2πC.2![]() πD.4π
πD.4π
查看答案和解析>>
科目:初中数学 来源: 题型:
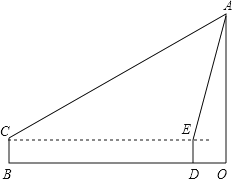
【题目】我市最近开通了“1号水路”观光游览专线,某中学数学活动小组带上高度为1.6m的测角仪,对其标志性建筑AO进行测量高度的综合实践活动,如图,在BC处测得直立于地面的AO顶点A的仰角为30°,然后前进20m至DE处,测得顶点A的仰角为75°.
(1)求AE的长(结果保留根号);
(2)求高度AO(精确到个位,参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°.小聪同学利用直尺和圆规完成了如下作图:
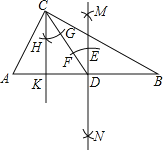
①分别以点A,B为圆心,以大于![]() AB长为半径画弧,两弧交于点M,N,过点M,N作直线与AB交于点D;
AB长为半径画弧,两弧交于点M,N,过点M,N作直线与AB交于点D;
②连接CD,以点D为圆心,以一定长为半径画弧,交MN于点E,交CD于点F,以点C为圆心,以同样定长为半径画弧,与CD交于点G,以点G为圆心,以EF长为半径画弧与前弧交于点H.作射线CH与AB交于点K,请根据以上操作,解答下列问题
(1)由尺规作图可知:直线MN是线段AB的 线,∠DCK= .
(2)若CD=5,AK=2,求CK的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
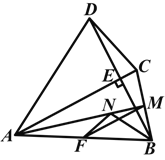
【题目】(2014山东淄博)如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
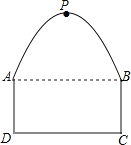
【题目】一座隧道的截面由抛物线和长方形的构成,长方形的长为8米,宽为2米,隧道的最高点P位于AB的中央且距地面6m.
(1)建立适当的直角坐标系,求抛物线解析式;
(2)如果隧道为单行道,一辆货车高4米,宽3米,能否从隧道内通过,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
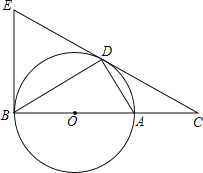
(1)求证:CD2=CACB;
(2)求证:CD是⊙O的切线;
(3)过点B作⊙O的切线交CD的延长线于点E,若BC=12,tan∠CDA=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+bx+c的图象经过坐标原点O和点A(7,0),直线AB交y轴于点B(0,﹣7),动点C(x,y)在直线AB上,且1<x<7,过点C作x轴的垂线交抛物线于点D,则CD的最值情况是( )
A.有最小值9B.有最大值9C.有最小值8D.有最大值8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com