
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
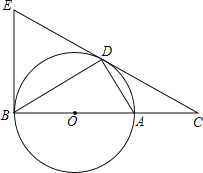
(1)求证:CD2=CACB;
(2)求证:CD是⊙O的切线;
(3)过点B作⊙O的切线交CD的延长线于点E,若BC=12,tan∠CDA=![]() ,求BE的长.
,求BE的长.
【答案】(1)见解析;(2)见解析;(3)BE的长为5.
【解析】
(1)通过相似三角形(△ADC∽△DBC)的对应边成比例来证得结论.
(2)如图,连接OD.欲证明CD是⊙O的切线,只需证明CD⊥OA即可.
(3)通过相似三角形△EBC∽△ODC的对应边成比例列出关于BE的方程,通过解方程来求线段BE的长度即可.
解:(1)证明:∵∠CDA=∠CBD,∠C=∠C,
∴△ADC∽△DBC,
∴![]() ,即CD2=CACB.
,即CD2=CACB.
(2)证明:如图,连接OD,

∵AB是⊙O的直径,
∴∠ADB=90°.
∴∠1+∠3=90°.
∵OA=OD,
∴∠2=∠3.
∴∠1+∠2=90°.
又∵∠CDA=∠CBD,即∠4=∠1,
∴∠4+∠2=90°,即∠CDO=90°.
∴OD⊥OA.
又∵OA是⊙O的半径,
∴CD是⊙O的切线.
(3)如图,连接OE,
∵EB、CD均为⊙O的切线,
∴ED=EB,OE⊥DB.
∴∠ABD+∠DBE=90°,∠OEB+∠DBE=90°.
∴∠ABD=∠OEB.
∴∠CDA=∠OEB.
∵tan∠CDA=![]() ,
,
∴![]() .
.
∵Rt△CDO∽Rt△CBE,
∴![]() .
.
∵BC=12,
∴CD=8.
在Rt△CBE中,设BE=x,
∴(x+8)2=x2+122,解得x=5.
∴BE的长为5.


科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线相交于点O,且AD>AB,过点O作OE⊥AC交AD于点E,连接CE.若平行四边形ABCD的周长为20,则△CDE的周长是( )
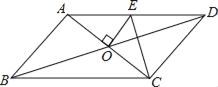
A. 10B. 11C. 12D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论:①BE=2AE;②△DFP~△BPH;③![]() ;④DP2=PHPC;其中正确的是( )
;④DP2=PHPC;其中正确的是( )
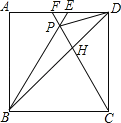
A. ①②③④B. ①③④C. ②③D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对今年“元旦”期间销售A、B、C三种品牌的绿色鸡蛋情况进行了统计,并绘制如图所示的扇形统计图和条形统计图.根据图中信息解答下列问题:
(1)该超市“元旦”期间共销售 个绿色鸡蛋,A品牌绿色鸡蛋在扇形统计图中所对应的扇形圆心角是 度;
(2)补全条形统计图;
(3)如果该超市的另一分店在“元旦”期间共销售这三种品牌的绿色鸡蛋1500个,请你估计这个分店销售的B种品牌的绿色鸡蛋的个数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD,DE,直接写出△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三名快递员某天的工作情况如图所示,其中点![]() ,
,![]() ,
,![]() 的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数;点
的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数;点![]() ,
,![]() ,
,![]() ,的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数.有如下三个结论:①上午派送快递所用时间最短的是甲;②下午派送快递件数最多的是丙;③在这一天中派送快递总件数最多的是乙.上述结论中,所有正确结论的序号是( )
,的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数.有如下三个结论:①上午派送快递所用时间最短的是甲;②下午派送快递件数最多的是丙;③在这一天中派送快递总件数最多的是乙.上述结论中,所有正确结论的序号是( )
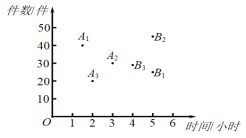
A. ①②B. ①③C. ②D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知P(x1,y1)Q(x2,y2),定义P、Q两点的横坐标之差的绝对值与纵坐标之差的绝对值的和为P、Q两点的直角距离,记作d(P,Q).即d(P,Q)=|x2﹣x1|+|y2﹣y1|
如图1,在平面直角坐标系xOy中,A(1,4),B(5,2),则d(A,B)=|5﹣1|+|2﹣4|=6.
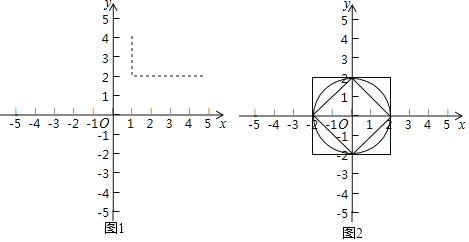
(1)如图2,已知以下三个图形:
①以原点为圆心,2为半径的圆;
②以原点为中心,4为边长,且各边分别与坐标轴垂直的正方形;
③以原点为中心,对角线分别在两条坐标轴上,对角线长为4的正方形.
点P是上面某个图形上的一个动点,且满足d(O,P)=2总成立.写出符合题意的图形对应的序号 .
(2)若直线y=k(x+3)上存在点P使得d(O,P)=2,求k的取值范围.
(3)在平面直角坐标系xOy中,P为动点,且d(O,P)=3,⊙M圆心为M(t,0),半径为1.若⊙M上存在点N使得PN=1,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O是坐标原点.点A在x轴的正半轴上,点A的坐标为(10,0).一条抛物线![]() 经过O,A,B三点,直线AB的表达式为
经过O,A,B三点,直线AB的表达式为![]() ,且与抛物线的对称轴交于点Q.
,且与抛物线的对称轴交于点Q.
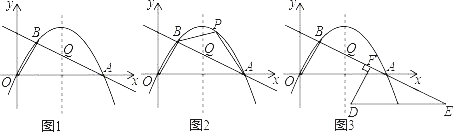
(1)求抛物线的表达式;
(2)如图2,在A,B两点之间的抛物线上有一动点P,连结AP,BP,设点P的横坐标为m,△ABP的面积S,求出面积S取得最大值时点P的坐标;
(3)如图3,将△OAB沿射线BA方向平移得到△DEF,在平移过程中,以A,D,Q为顶点的三角形能否成为等腰三角形?如果能,请直接写出此时点E的坐标(点O除外);如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com