
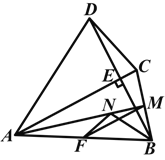
【题目】(2014山东淄博)如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.
【答案】见解析
【解析】
解:(1)△BMN是等腰直角三角形.
证明:∵AB=AC,点M是BC的中点,
∴AM⊥BC,AM平分∠BAC.
∵BN平分∠ABE,AC⊥BD,
∴∠AEB=90°,
∴∠EAB+∠EBA=90°,
∴![]() .
.
∴△BMN是等腰直角三角形.
(2)△MFN∽△BDC.
证明:∵点F,M分别是AB,BC的中点,
∴FM∥AC,![]() .
.
∵AC=BD,
∴![]() ,即
,即![]() .
.
由(1)知△BMN是等腰直角三角形,
∴![]() ,即
,即![]() ,
,
∴![]() .
.
∵AM⊥BC,
∴∠NMF+∠FMB=90°.
∵FM∥AC.
∵∠ACB=∠FMB.
∵∠CEB=90°,
∴∠ACB+∠CBD=90°.
∴∠CBD+∠FMB=90°,
∴∠NMF=∠CBD.
∴△MFN∽△BDC.


科目:初中数学 来源: 题型:
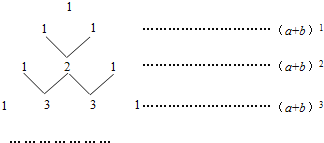
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左、右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等.
(1)(a+b)n展开式中项数共有 项.
(2)写出(a+b)5的展开式:(a+b)5= .
(3)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以每秒
以每秒![]() 个单位长度的速度运动;点
个单位长度的速度运动;点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以每秒
以每秒![]() 个单位长度的速度运动.如果
个单位长度的速度运动.如果![]() ,
,![]() 同时出发,用
同时出发,用![]() 秒表示运动的时间.
秒表示运动的时间.

请解答下列问题:
(1)当![]() 为何值时,
为何值时,![]() 是等腰直角三角形?
是等腰直角三角形?
(2)当![]() t为何值时,以点
t为何值时,以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了改善办公条件,计划从厂家购买![]() 两种型号电脑.已知每台
两种型号电脑.已知每台![]() 种型号电脑价格比每台
种型号电脑价格比每台![]() 种型号电脑价格多0.1万元,且用10万元购买
种型号电脑价格多0.1万元,且用10万元购买![]() 种型号电脑的数量与用8万购买
种型号电脑的数量与用8万购买![]() 种型号电脑的数量相同.
种型号电脑的数量相同.
(1)求![]() 两种型号电脑每台价格各为多少万元?
两种型号电脑每台价格各为多少万元?
(2)学校预计用不多于9.2万元的资金购进这两种电脑共20台,其中![]() 种型号电脑至少要购进10台,请问有哪几种购买方案?
种型号电脑至少要购进10台,请问有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=5,E是BC边上的一个动点,DF⊥AE,垂足为点F,连结CF
(1)若AE=BC
①求证:△ABE≌△DFA;②求四边形CDFE的周长;③求tan∠FCE的值;
(2)探究:当BE为何值时,△CDF是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y1=ax2+bx+c(a,b,c为常数)的图象如图所示,若y1+y2=2,则下列关于函数y2的图象与性质描述正确的是:( )

A.函数y2的图象开口向上
B.函数y2的图象与x轴没有公共点
C.当x>2时,y2随x的增大而减小
D.当x=1时,函数y2的值小于0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某景区每日利润y1(元)与当天游客人数x(人)的函数图像.为了吸引游客,该景区决定改革,改革后每张票价减少20元,运营成本减少800元.设改革后该景区每日利润为y2(元).(注:每日利润=票价收入-运营成本)
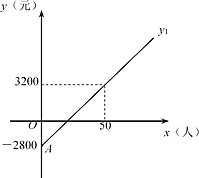
(1)解释点A的实际意义:______.
(2)分别求出y1、y2关于x的函数表达式;
(3)当游客人数为多少人时,改革前的日利润与改革后的日利润相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
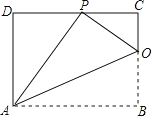
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于点O,连接AP、OP、OA.
(1)求证:![]() ;
;
(2)若△OCP与△PDA的面积比为1:4,求边AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购买A、B两种奖品,奖励成绩优异的同学.已知购买1件A奖品和1件B奖品共需18元;购买30件A奖品和20件B奖品共需480元.
(1)A、B两种奖品的单价分别是多少元?
(2)如果学校购买两种奖品共100件,总费用不超过850元,那么最多可以购买A奖品多少件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com