
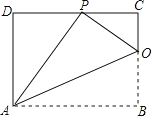
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于点O,连接AP、OP、OA.
(1)求证:![]() ;
;
(2)若△OCP与△PDA的面积比为1:4,求边AB的长.
【答案】(1)详见解析;(2)10.
【解析】
①只需证明两对对应角分别相等可得两个三角形相似;故![]() .
.
②根据相似三角形的性质求出PC长以及AP与OP的关系,然后在Rt△PCO中运用勾股定理求出OP长,从而求出AB长.
①∵四边形ABCD是矩形,
∴AD=BC,DC=AB,∠DAB=∠B=∠C=∠D=90°.
由折叠可得:AP=AB,PO=BO,∠PAO=∠BAO,∠APO=∠B.
∴∠APO=90°.
∴∠APD=90°∠CPO=∠POC.
∵∠D=∠C,∠APD=∠POC.
∴△OCP∽△PDA.
∴![]() .
.
②∵△OCP与△PDA的面积比为1:4,
∴OCPD=OPPA=CPDA=14√=12.
∴PD=2OC,PA=2OP,DA=2CP.
∵AD=8,
∴CP=4,BC=8.
设OP=x,则OB=x,CO=8x.
在△PCO中,
∵∠C=90,CP=4,OP=x,CO=8x,
∴x2=(8x)2+42.
解得:x=5.
∴AB=AP=2OP=10.
∴边AB的长为10.


科目:初中数学 来源: 题型:
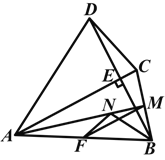
【题目】(2014山东淄博)如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(﹣3,1),B(0,3),C(0,1)

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1、BA1后,求四边形AB1A1B的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图山坡上有一根旗杆AB,旗杆底部B点到山脚C点的距离BC为![]() 米,斜坡BC的坡度i=1:
米,斜坡BC的坡度i=1: ![]() .小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.
.小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.
(1)求坡角∠BCD;
(2)求旗杆AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象相交于点A(a,3),且与x轴相交于点B.
的图象相交于点A(a,3),且与x轴相交于点B.
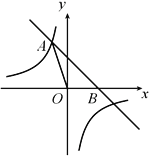
(1)求该反比例函数的表达式;(2)若P为y轴上的点,且△AOP的面积是△AOB的面积的![]() ,请直接写出点P的坐标.
,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
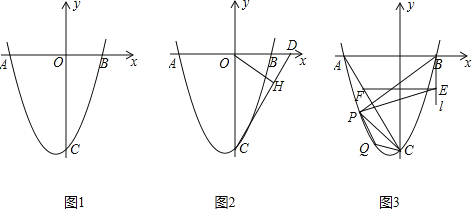
【题目】如图1,抛物线![]() 交x轴于点
交x轴于点![]() ,
,![]() ,交y轴于点C.
,交y轴于点C.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 如图2,D点坐标为
如图2,D点坐标为![]() ,连结
,连结![]() 若点H是线段DC上的一个动点,求
若点H是线段DC上的一个动点,求![]() 的最小值.
的最小值.
![]() 如图3,连结AC,过点B作x轴的垂线l,在第三象限中的抛物线上取点P,过点P作直线AC的垂线交直线l于点E,过点E作x轴的平行线交AC于点F,已知
如图3,连结AC,过点B作x轴的垂线l,在第三象限中的抛物线上取点P,过点P作直线AC的垂线交直线l于点E,过点E作x轴的平行线交AC于点F,已知![]() .
.
![]() 求点P的坐标;
求点P的坐标;
![]() 在抛物线
在抛物线![]() 上是否存在一点Q,使得
上是否存在一点Q,使得![]() 成立?若存在,求出Q点坐标;若不存在,请说明理由.
成立?若存在,求出Q点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,F为AD上一点,且BF=BD.BF的延长线交AC于点E.
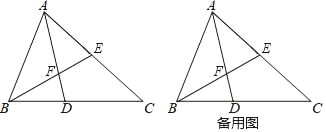
(1)求证:ABAD=AFAC;
(2)若∠BAC=60°.AB=4,AC=6,求DF的长;
(3)若∠BAC=60°,∠ACB=45°,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
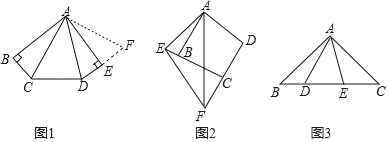
【题目】(1)如图1,在五边形ABCDE中,AB=AE,∠B=∠BAE=∠AED=90°,∠CAD=45°,试猜想BC,CD,DE之间的数量关系.小明经过仔细思考,得到如下解题思路:
将△ABC绕点A逆时针旋转90°至△AEF,由∠B=∠AED=90°,得∠DEF=180°,即点D,E,F三点共线,易证△ACD≌ ,故BC,CD,DE之间的数量关系是 ;
(2)如图2,在四边形ABCD中,AB=AD,∠ABC+∠D=180°,点E,F分别在边CB,DC的延长线上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
(3)如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°,若BD=2,CE=3,则DE的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com