
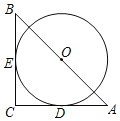
【题目】如图,在Rt△ABC中,∠C=90°,AB=4![]() ,以AB的中点O为圆心作圆,圆O分别与AC、BC相切于点D、E两点,则弧DE的长为__.
,以AB的中点O为圆心作圆,圆O分别与AC、BC相切于点D、E两点,则弧DE的长为__.
【答案】π.
【解析】
连接OE,OD,根据切线的性质得到OE⊥BC,OD⊥AC,推出矩形OECD是正方形,得到CE=CD,∠EOD=90°,根据全等三角形的性质得到BE=OD,OE=AD,求得BE=OE=OD=AD,根据等腰直角三角形的性质得到AB=4![]() ,求得OE=OD=2,根据弧长公式即可得到结论.
,求得OE=OD=2,根据弧长公式即可得到结论.
连接OE,OD,
∵圆O分别与AC、BC相切于点D、E两点,
∴OE⊥BC,OD⊥AC,
∵∠C=90°,
∴四边形OECD是矩形,
∵OE=OD,
∴矩形OECD是正方形,
∴CE=CD,∠EOD=90°,
∴∠B+∠BOE=∠BOE+∠AOD=90°,
∴∠B=∠AOD,
∵∠BEO=∠ADO=90°,OB=OA,
∴△BOE≌△OAD(AAS),
∴BE=OD,OE=AD,
∴BE=OE=OD=AD,
∴∠B=∠A=45°,
∵AB=4![]() ,
,
∴OE=OD=2,
∴弧DE的长=![]() ,
,
故答案为:π.



科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
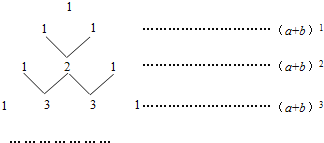
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左、右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等.
(1)(a+b)n展开式中项数共有 项.
(2)写出(a+b)5的展开式:(a+b)5= .
(3)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
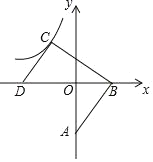
【题目】如图,已知直线AB分别交x轴和y轴与B、A两点,A(0,﹣3),B(2,0).
(1)求出直线AB的解析式;
(2)将线段AB平移至DC的位置,其D点在x轴的负半轴上,C点在反比例函数y=![]() 的图象上,若S△BCD=18,则反比例函数解析式为____;
的图象上,若S△BCD=18,则反比例函数解析式为____;
(3)设BC交y轴于P,求S△ABP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一游客步行从宾馆C出发,沿北偏东60°的方向行走到1000米的人民公园A处,参观后又从A处沿正南方向行走一段距离到达位于宾馆南偏东45°方向的净业寺B处,如图所示.
(1)求这名游客从人民公园到净业寺的途中到宾馆的最短距离;
(2)若这名游客以80米/分的速度从净业寺返回宾馆,那么他能在10分钟内到达宾馆吗?请通过计算说明理由.(假设游客行走的路线均是沿直线行走的)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以每秒
以每秒![]() 个单位长度的速度运动;点
个单位长度的速度运动;点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以每秒
以每秒![]() 个单位长度的速度运动.如果
个单位长度的速度运动.如果![]() ,
,![]() 同时出发,用
同时出发,用![]() 秒表示运动的时间.
秒表示运动的时间.

请解答下列问题:
(1)当![]() 为何值时,
为何值时,![]() 是等腰直角三角形?
是等腰直角三角形?
(2)当![]() t为何值时,以点
t为何值时,以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了改善办公条件,计划从厂家购买![]() 两种型号电脑.已知每台
两种型号电脑.已知每台![]() 种型号电脑价格比每台
种型号电脑价格比每台![]() 种型号电脑价格多0.1万元,且用10万元购买
种型号电脑价格多0.1万元,且用10万元购买![]() 种型号电脑的数量与用8万购买
种型号电脑的数量与用8万购买![]() 种型号电脑的数量相同.
种型号电脑的数量相同.
(1)求![]() 两种型号电脑每台价格各为多少万元?
两种型号电脑每台价格各为多少万元?
(2)学校预计用不多于9.2万元的资金购进这两种电脑共20台,其中![]() 种型号电脑至少要购进10台,请问有哪几种购买方案?
种型号电脑至少要购进10台,请问有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
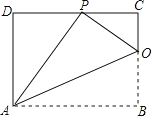
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于点O,连接AP、OP、OA.
(1)求证:![]() ;
;
(2)若△OCP与△PDA的面积比为1:4,求边AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com