
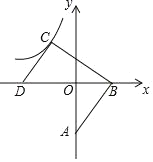
【题目】如图,已知直线AB分别交x轴和y轴与B、A两点,A(0,﹣3),B(2,0).
(1)求出直线AB的解析式;
(2)将线段AB平移至DC的位置,其D点在x轴的负半轴上,C点在反比例函数y=![]() 的图象上,若S△BCD=18,则反比例函数解析式为____;
的图象上,若S△BCD=18,则反比例函数解析式为____;
(3)设BC交y轴于P,求S△ABP.
【答案】(1)y=![]() x﹣3;(2)y=﹣
x﹣3;(2)y=﹣![]() ;(3)S△ABP=3.6.
;(3)S△ABP=3.6.
【解析】
(1)利用待定系数法代入A、B坐标即可求得AB解析式
(2)利用平移可设得D点坐标为(xD,0),C点坐标为(xD+2,3),根据S△BCD=18,可得![]() |(xD﹣2)|×3=18.求得点C、D坐标,将点C代入反比例函数解析式即可求解.
|(xD﹣2)|×3=18.求得点C、D坐标,将点C代入反比例函数解析式即可求解.
(3)先利用点B、C坐标求得BC所在直线解析式,求得点P坐标,进而利用三角形面积公式求解.
解:(1)设直线AB的解析式为:y=kx+b(k≠0),
∵A(0,﹣3),B(2,0),
∴![]() ,
,
解得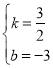 ,
,
∴直线AB的解析式为y=![]() x﹣3;
x﹣3;
(2)∵A(0,﹣3),B(2,0),
∴将线段AB平移至DC的位置,D点坐标为(xD,0),C点坐标为(xD+2,3).
又S△BCD=![]() BD×3=18,
BD×3=18,
∴![]() |(xD﹣2)|×3=18.
|(xD﹣2)|×3=18.
∴xD=﹣10.
则点D(﹣10,0),点C为(﹣8,3).
又C点在反比例函数y=![]() 的图象上,
的图象上,
∴k=﹣8×3=﹣24.
∴反比例函数解析式为y=﹣![]()
故答案为:y=﹣![]() ;
;
(3)设直线BC的解析式为y=ax+c,
∵B(2,0),C(﹣8,3),
∴![]() ,解得
,解得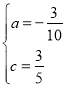 ,
,
∴直线BC的解析式为y=﹣![]() x+
x+![]() ,
,
∴P(0,![]() ),
),
∴AP=3.6,
∴S△ABP=![]() ×3.6×2=3.6.
×3.6×2=3.6.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
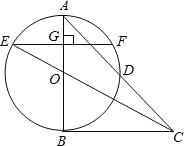
【题目】如图,在△ABC中,∠A=45°,以AB为直径的⊙O交于AC的中点D,连接CO,CO的延长线交⊙O于点E,过点E作EF⊥AB,垂足为点G.
(1)求证:BC时⊙O的切线;
(2)若AB=2,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分7分)某中学要在全校学生中举办“中国梦·我的梦”主题演讲比赛,要求每班一
名代表参赛,九年级(1)班经过投票初选,小亮和小丽票数并列班级第一,现在他们都想代表本班参赛,
经班长与他们协商决定,用他们学过的掷骰子游戏来确定谁去参赛(胜者参赛)。规则如下:两人同时随机
各掷一枚完全相同且质地均匀的骰子一次,向上一面的点数都是奇数,则小亮胜;向上一面的点数都是偶
数,则小丽胜;否则,视为平局,若为平局,继续上述游戏,直至分出胜负为止。如果小亮和小丽按上述
规则各掷一次骰子,那么请你解答下列问题:
(1)小亮掷得向上一面的点数为奇数的概率是多少?
(2)该游戏是否公平?请用列表或树状图等方法说明理由。(骰子:六个面上分别刻有1、2、3、4、5、6 个小圆点的小正方体)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194.现用一名身高为186cm的队员换下场上身高为192cm的队员,与换人前相比,场上队员的身高( )
A. 平均数变小,中位数变小
B. 平均数变小,中位数变大
C. 平均数变大,中位数变小
D. 平均数变大,中位数变大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在全校范围内随机抽取了一部分学生进行“风味泰兴﹣﹣我最喜爱的泰兴美食”调查活动,将调查问卷整理后绘制成如下图所示的不完整的条形统计图和扇形统计图.
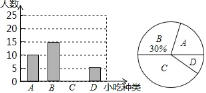
调查问卷在下面四种泰兴美食中,你最喜爱的是( )(单选)
A.黄桥烧饼 B.宣堡小馄饨C.蟹黄汤包 D.刘陈猪四宝
请根据所给信息解答下列问题:
(1)本次抽样调查的样本容量是 ;
(2)补全条形统计图,并计算扇形统计图中“A”部分所对应的圆心角的度数为 ;
(3)若全校有1200名学生,请估计全校学生中最喜爱“蟹黄汤包”的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春平中学要为学校科技活动小组提供实验器材,计划购买A型、B型两种型号的放大镜.若购买8个A型放大镜和5个B型放大镜需用220元;若购买4个A型放大镜和6个B型放大镜需用152元.
(1)求每个A型放大镜和每个B型放大镜各多少元;
(2)春平中学决定购买A型放大镜和B型放大镜共75个,总费用不超过1180元,那么最多可以购买多少个A型放大镜?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(﹣3,1),B(0,3),C(0,1)

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1、BA1后,求四边形AB1A1B的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com