
【题目】(本题满分7分)某中学要在全校学生中举办“中国梦·我的梦”主题演讲比赛,要求每班一
名代表参赛,九年级(1)班经过投票初选,小亮和小丽票数并列班级第一,现在他们都想代表本班参赛,
经班长与他们协商决定,用他们学过的掷骰子游戏来确定谁去参赛(胜者参赛)。规则如下:两人同时随机
各掷一枚完全相同且质地均匀的骰子一次,向上一面的点数都是奇数,则小亮胜;向上一面的点数都是偶
数,则小丽胜;否则,视为平局,若为平局,继续上述游戏,直至分出胜负为止。如果小亮和小丽按上述
规则各掷一次骰子,那么请你解答下列问题:
(1)小亮掷得向上一面的点数为奇数的概率是多少?
(2)该游戏是否公平?请用列表或树状图等方法说明理由。(骰子:六个面上分别刻有1、2、3、4、5、6 个小圆点的小正方体)
【答案】(1)![]() ;(2)游戏公平.
;(2)游戏公平.
【解析】
试题(1)根据概率的求法,找准两点:①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.骰子共六种情况,其中奇数3种.
(2)根据题意画出树状图或列表,由图表求得所有等可能的结果与恰好匹配的情况,利用概率公式分别求出小亮和小丽的概率比较大小,如果概率相等则公平否则不公平.
试题解析:(1)所求概率P=![]() =
=![]()
(2)游戏公平.
理由如下
1 | 2 | 3 | 4 | 5 | 6 | |
1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) |
2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
由表格可知共有36种等可能的结果,其中小亮和小丽获胜各有9种情况,
所以![]() =
=![]() ,
,![]() =
=![]()
所以游戏公平.


科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片ABCD中,E,F分别是AD,BC的中点,沿过点B的直线折叠,使点C落在EF上,落点为N,折痕交CD边于点M,BM与EF交于点P,再展开.则下列结论中:①CM=DM;②∠ABN=30°;③AB2=3CM2;④△PMN是等边三角形.
正确的有( )
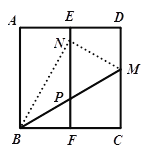
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
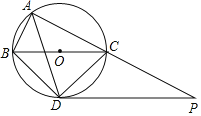
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△ABD∽△DCP;
(3)当AB=5cm,AC=12cm时,求线段PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某电视台的一档选秀节目中,有三位评委,每位评委在选手完成才艺表演后,出示“通过”(用√表示)或“淘汰”(用×表示)的评定结果,节目组规定:每位选手至少获得两位评委的“通过”才能晋级.
(1)请用树状图列举出选手A获得三位评委评定的各种可能的结果;
(2)求选手A晋级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是_____.
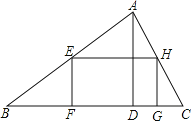
查看答案和解析>>
科目:初中数学 来源: 题型:
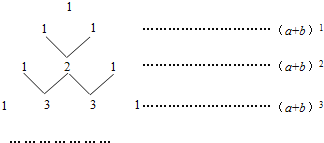
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左、右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等.
(1)(a+b)n展开式中项数共有 项.
(2)写出(a+b)5的展开式:(a+b)5= .
(3)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
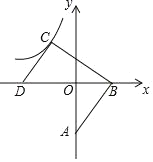
【题目】如图,已知直线AB分别交x轴和y轴与B、A两点,A(0,﹣3),B(2,0).
(1)求出直线AB的解析式;
(2)将线段AB平移至DC的位置,其D点在x轴的负半轴上,C点在反比例函数y=![]() 的图象上,若S△BCD=18,则反比例函数解析式为____;
的图象上,若S△BCD=18,则反比例函数解析式为____;
(3)设BC交y轴于P,求S△ABP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了改善办公条件,计划从厂家购买![]() 两种型号电脑.已知每台
两种型号电脑.已知每台![]() 种型号电脑价格比每台
种型号电脑价格比每台![]() 种型号电脑价格多0.1万元,且用10万元购买
种型号电脑价格多0.1万元,且用10万元购买![]() 种型号电脑的数量与用8万购买
种型号电脑的数量与用8万购买![]() 种型号电脑的数量相同.
种型号电脑的数量相同.
(1)求![]() 两种型号电脑每台价格各为多少万元?
两种型号电脑每台价格各为多少万元?
(2)学校预计用不多于9.2万元的资金购进这两种电脑共20台,其中![]() 种型号电脑至少要购进10台,请问有哪几种购买方案?
种型号电脑至少要购进10台,请问有哪几种购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com