
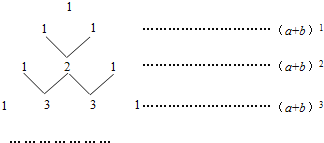
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左、右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等.
(1)(a+b)n展开式中项数共有 项.
(2)写出(a+b)5的展开式:(a+b)5= .
(3)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1.
【答案】(1)n+1;(2)a5+5a4b+10a3b2+10a2b3+5ab4+b5;(3)1.
【解析】
(1)根据规律,可知n+1项;
(2)根据规律,可知(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
(3)根据规律得出原式=(2﹣1)5.
解:(1))(a+b)n展开式中项数共有n+1项,
故答案为n+1;
(2)(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
故答案为a5+5a4b+10a3b2+10a2b3+5ab4+b5
(3)25﹣5×24+10×23﹣10×22+5×2﹣1
=25+5×24×(﹣1)+10×23×(﹣1)2+10×22×(﹣1)3+5×2×(﹣1)4+(﹣1)5
=(2﹣1)5
=1.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
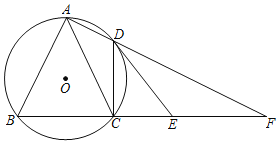
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,AD、BC的延长线交于点F,点E在CF上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)当AB=AC时,若CE=4,EF=6,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购进甲、乙两种规格的书架,经市场调查发现有线上和线下两种购买方式,具体情况如下表:
规格 | 线下 | 线上 | ||
单价(元/个) | 运费(元/个) | 单价(元/个) | 运费(元/个) | |
甲 | 240 | 0 | 210 | 20 |
乙 | 300 | 0 | 250 | 30 |
(1)如果在线下购买甲、乙两种书架共30个,花费8280元,求甲、乙两种书架各购买了多少个?
(2)如果在线上购买甲、乙两种书架共30个,且购买乙种书架的数量不少于甲种书架的3倍,请求出花费最少的购买方案及花费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分7分)某中学要在全校学生中举办“中国梦·我的梦”主题演讲比赛,要求每班一
名代表参赛,九年级(1)班经过投票初选,小亮和小丽票数并列班级第一,现在他们都想代表本班参赛,
经班长与他们协商决定,用他们学过的掷骰子游戏来确定谁去参赛(胜者参赛)。规则如下:两人同时随机
各掷一枚完全相同且质地均匀的骰子一次,向上一面的点数都是奇数,则小亮胜;向上一面的点数都是偶
数,则小丽胜;否则,视为平局,若为平局,继续上述游戏,直至分出胜负为止。如果小亮和小丽按上述
规则各掷一次骰子,那么请你解答下列问题:
(1)小亮掷得向上一面的点数为奇数的概率是多少?
(2)该游戏是否公平?请用列表或树状图等方法说明理由。(骰子:六个面上分别刻有1、2、3、4、5、6 个小圆点的小正方体)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+bx+c经过点B(2
x2+bx+c经过点B(2![]() ,0)、C(0,2)两点,与x轴的另一个交点为A.
,0)、C(0,2)两点,与x轴的另一个交点为A.
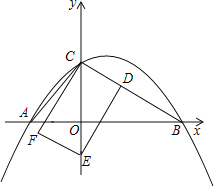
(1)求抛物线的解析式;
(2)点D从点C出发沿线段CB以每秒![]() 个单位长度的速度向点B运动,作DE⊥CB交y轴于点E,以CD、DE为边作矩形CDEF,设点D运动时间为t(s).
个单位长度的速度向点B运动,作DE⊥CB交y轴于点E,以CD、DE为边作矩形CDEF,设点D运动时间为t(s).
①当点F落在抛物线上时,求t的值;
②若点D在运动过程中,设△ABC与矩形CDEF重叠部分的面积为S,请直接写出S与t之间的函数关系式,并写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194.现用一名身高为186cm的队员换下场上身高为192cm的队员,与换人前相比,场上队员的身高( )
A. 平均数变小,中位数变小
B. 平均数变小,中位数变大
C. 平均数变大,中位数变小
D. 平均数变大,中位数变大
查看答案和解析>>
科目:初中数学 来源: 题型:
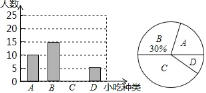
【题目】某数学兴趣小组在全校范围内随机抽取了一部分学生进行“风味泰兴﹣﹣我最喜爱的泰兴美食”调查活动,将调查问卷整理后绘制成如下图所示的不完整的条形统计图和扇形统计图.
调查问卷在下面四种泰兴美食中,你最喜爱的是( )(单选)
A.黄桥烧饼 B.宣堡小馄饨C.蟹黄汤包 D.刘陈猪四宝
请根据所给信息解答下列问题:
(1)本次抽样调查的样本容量是 ;
(2)补全条形统计图,并计算扇形统计图中“A”部分所对应的圆心角的度数为 ;
(3)若全校有1200名学生,请估计全校学生中最喜爱“蟹黄汤包”的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
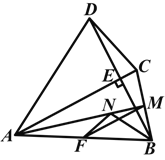
【题目】(2014山东淄博)如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com