
【题目】如图,抛物线y=﹣![]() x2+bx+c经过点B(2
x2+bx+c经过点B(2![]() ,0)、C(0,2)两点,与x轴的另一个交点为A.
,0)、C(0,2)两点,与x轴的另一个交点为A.
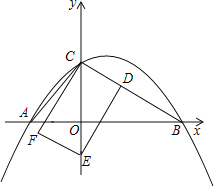
(1)求抛物线的解析式;
(2)点D从点C出发沿线段CB以每秒![]() 个单位长度的速度向点B运动,作DE⊥CB交y轴于点E,以CD、DE为边作矩形CDEF,设点D运动时间为t(s).
个单位长度的速度向点B运动,作DE⊥CB交y轴于点E,以CD、DE为边作矩形CDEF,设点D运动时间为t(s).
①当点F落在抛物线上时,求t的值;
②若点D在运动过程中,设△ABC与矩形CDEF重叠部分的面积为S,请直接写出S与t之间的函数关系式,并写出自变量t的取值范围.
【答案】(1)![]() ;(2)①
;(2)①![]() ②
②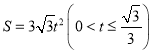 ,
,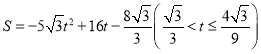 ,
,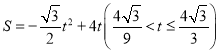
【解析】
(1)把B、C的坐标代入抛物线的解析式求解即可;
(2)①点F在抛物线上,作DG⊥y轴,FH⊥y轴,证明△CDG≌△EFH,根据全等三角形的性质有CG=HE,GD=FH,证明△CGD∽△COB,根据相似三角形的性质得到![]() 表示出OH的长度,即可求得点F的坐标,最后将点F的坐标代入抛物线的解析式求解即可;
表示出OH的长度,即可求得点F的坐标,最后将点F的坐标代入抛物线的解析式求解即可;
②当![]() 时,S=CDDE;当
时,S=CDDE;当![]() 时,S=矩形DEGF的面积-△GEH的面积.当
时,S=矩形DEGF的面积-△GEH的面积.当![]() 时,
时,![]()
解:(1)把![]() 两点代入抛物线解析式得:
两点代入抛物线解析式得:
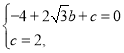
解得:![]()
则抛物线解析式为![]()
(2)①如图1所示,点F在抛物线上,作DG⊥y轴,FH⊥y轴,
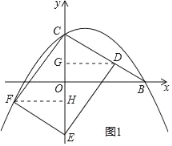
易得△CDG≌△EFH,即CG=HE,GD=FH,
由题意得:![]()
∵△CGD∽△COB,
∴![]()
即![]()
![]()
∴OH=![]() ,即
,即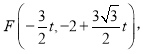
代入抛物线解析式得: ![]()
解得:t=![]() ;
;
②分三种情况考虑:
(i)如图2所示,△ABC与矩形CDEF重叠部分为矩形CDEF,
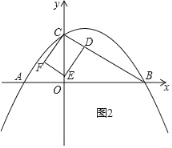
在Rt△CDE中,![]()
∴DE=3t,
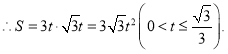
(ii)如图3所示,△ABC与矩形CDEF重叠部分为五边形CDHGF,
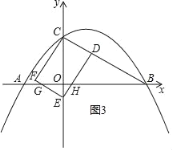
由题意得:![]()
在Rt△CED中,∠ECD=60°,
∴![]()
∴![]()
在Rt△OGE中,![]()
同理可得![]() 即
即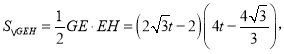
则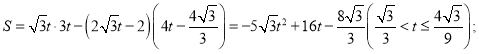
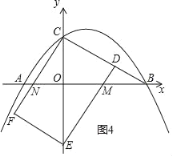
(iii)如图4,△ABC与矩形CDEF重叠部分为四边形CDMN,
由题意得: 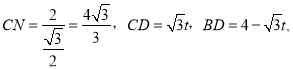
在Rt△BMD中, ![]()
则![]()
![]() ,
,
![]()
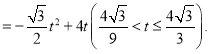


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】请认真阅读下面的数学小探究系列,完成所提出的问题:
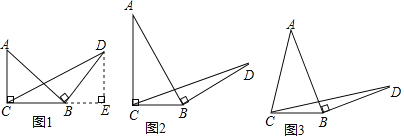
![]() 探究1:如图1,在等腰直角三角形ABC中,
探究1:如图1,在等腰直角三角形ABC中,![]() ,
,![]() ,将边AB绕点B顺时针旋转
,将边AB绕点B顺时针旋转![]() 得到线段BD,连接
得到线段BD,连接![]() 求证:
求证:![]() 的面积为
的面积为![]() 提示:过点D作BC边上的高DE,可证
提示:过点D作BC边上的高DE,可证![]() ≌
≌![]()
![]() 探究2:如图2,在一般的
探究2:如图2,在一般的![]() 中,
中,![]() ,
,![]() ,将边AB绕点B顺时针旋转
,将边AB绕点B顺时针旋转![]() 得到线段BD,连接
得到线段BD,连接![]() 请用含a的式子表示
请用含a的式子表示![]() 的面积,并说明理由.
的面积,并说明理由.
![]() 探究3:如图3,在等腰三角形ABC中,
探究3:如图3,在等腰三角形ABC中,![]() ,
,![]() ,将边AB绕点B顺时针旋转
,将边AB绕点B顺时针旋转![]() 得到线段BD,连接
得到线段BD,连接![]() 试探究用含a的式子表示
试探究用含a的式子表示![]() 的面积,要有探究过程.
的面积,要有探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
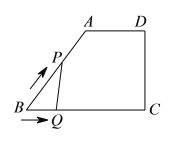
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,动点
,动点![]() ,
,![]() 同时从点
同时从点![]() 出发,点
出发,点![]() 以
以![]() 的速度沿折线
的速度沿折线![]() 运动到点
运动到点![]() ,点
,点![]() 以
以![]() 的速度沿
的速度沿![]() 运动到点
运动到点![]() ,设
,设![]() ,
,![]() 同时出发
同时出发![]() 时,
时,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的函数图象大致是( )
的函数图象大致是( )
A. 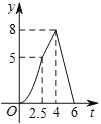 B.
B. 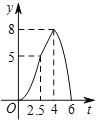
C. 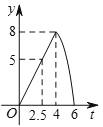 D.
D. 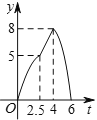
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某电视台的一档选秀节目中,有三位评委,每位评委在选手完成才艺表演后,出示“通过”(用√表示)或“淘汰”(用×表示)的评定结果,节目组规定:每位选手至少获得两位评委的“通过”才能晋级.
(1)请用树状图列举出选手A获得三位评委评定的各种可能的结果;
(2)求选手A晋级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解九年级学生体育测试成绩情况,以九年级(1)班学生的体育测试成绩为样本,按B、C、D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:90分﹣100分;B级:75分﹣89分;C级:60分~74分;D级:60分以下)
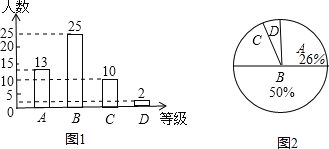
(1)求出D级学生的人数占全班总人数的百分比;
(2)求出扇形统计图(图2)中C级所在的扇形圆心角的度数;
(3)若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
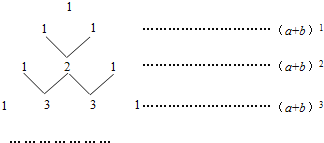
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左、右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等.
(1)(a+b)n展开式中项数共有 项.
(2)写出(a+b)5的展开式:(a+b)5= .
(3)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=5,E是BC边上的一个动点,DF⊥AE,垂足为点F,连结CF
(1)若AE=BC
①求证:△ABE≌△DFA;②求四边形CDFE的周长;③求tan∠FCE的值;
(2)探究:当BE为何值时,△CDF是等腰三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com