
【题目】如图是某景区每日利润y1(元)与当天游客人数x(人)的函数图像.为了吸引游客,该景区决定改革,改革后每张票价减少20元,运营成本减少800元.设改革后该景区每日利润为y2(元).(注:每日利润=票价收入-运营成本)
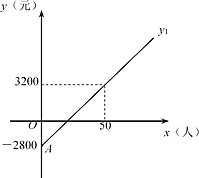
(1)解释点A的实际意义:______.
(2)分别求出y1、y2关于x的函数表达式;
(3)当游客人数为多少人时,改革前的日利润与改革后的日利润相等?
【答案】(1)改革前某景区每日运营成本为2800元;(2)y1=120x-2800;y2=100 x-2000.(3)40人
【解析】
(1)根据题意可得点A的实际意义是改革前某景区每日运营成本为2800元;(2)利用待定系数法即可求出y1关于x的函数表达式;进而根据票价减少20元,运营成本减少800元可得y2关于x的解析式;(3)令y1=y2,列方程求出x的值即可得答案.
(1)改革前某景区每日运营成本为2800元;
(2)设y1与x之间的函数表达式为y1=kx+b(k、b为常数,k≠0),
根据题意,当x=0时,y1=-2800;当x=50时,y1=3200.
所以![]() ,
,
解得![]() ,
,
所以,y1与x之间的函数表达式为y1=120x-2800.
根据题意,y2与x之间的函数表达式为y2=100x-2000.
(3)根据题意,当y1=y2时,得120x-2800=100x-2000.
解得x=40.
答:当游客人数为40人时,改革前的日利润与改革后的日利润相等.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在全校范围内随机抽取了一部分学生进行“风味泰兴﹣﹣我最喜爱的泰兴美食”调查活动,将调查问卷整理后绘制成如下图所示的不完整的条形统计图和扇形统计图.
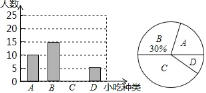
调查问卷在下面四种泰兴美食中,你最喜爱的是( )(单选)
A.黄桥烧饼 B.宣堡小馄饨C.蟹黄汤包 D.刘陈猪四宝
请根据所给信息解答下列问题:
(1)本次抽样调查的样本容量是 ;
(2)补全条形统计图,并计算扇形统计图中“A”部分所对应的圆心角的度数为 ;
(3)若全校有1200名学生,请估计全校学生中最喜爱“蟹黄汤包”的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )

A. (![]() ,0) B. (2,0) C. (
,0) B. (2,0) C. (![]() ,0) D. (3,0)
,0) D. (3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
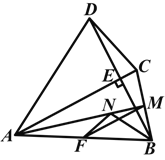
【题目】(2014山东淄博)如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
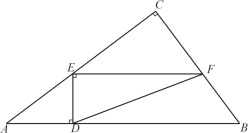
【题目】如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,D为AB边上的动点,过点D作DE⊥AB交边AC于点E,过点E作EF⊥DE交BC于点F,连接DF.
(1)当AD=4时,求EF的长度;
(2)求△DEF的面积的最大值;
(3)设O为DF的中点,随着点D的运动,则点O的运动路径的长度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(﹣3,1),B(0,3),C(0,1)

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1、BA1后,求四边形AB1A1B的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图山坡上有一根旗杆AB,旗杆底部B点到山脚C点的距离BC为![]() 米,斜坡BC的坡度i=1:
米,斜坡BC的坡度i=1: ![]() .小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.
.小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.
(1)求坡角∠BCD;
(2)求旗杆AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)

查看答案和解析>>
科目:初中数学 来源: 题型:
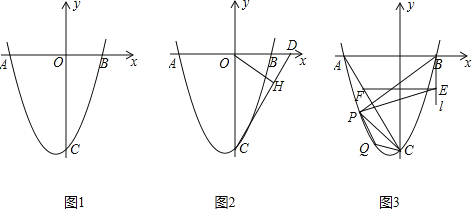
【题目】如图1,抛物线![]() 交x轴于点
交x轴于点![]() ,
,![]() ,交y轴于点C.
,交y轴于点C.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 如图2,D点坐标为
如图2,D点坐标为![]() ,连结
,连结![]() 若点H是线段DC上的一个动点,求
若点H是线段DC上的一个动点,求![]() 的最小值.
的最小值.
![]() 如图3,连结AC,过点B作x轴的垂线l,在第三象限中的抛物线上取点P,过点P作直线AC的垂线交直线l于点E,过点E作x轴的平行线交AC于点F,已知
如图3,连结AC,过点B作x轴的垂线l,在第三象限中的抛物线上取点P,过点P作直线AC的垂线交直线l于点E,过点E作x轴的平行线交AC于点F,已知![]() .
.
![]() 求点P的坐标;
求点P的坐标;
![]() 在抛物线
在抛物线![]() 上是否存在一点Q,使得
上是否存在一点Q,使得![]() 成立?若存在,求出Q点坐标;若不存在,请说明理由.
成立?若存在,求出Q点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
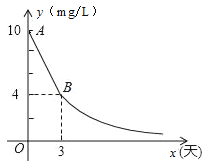
【题目】环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0 mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,其中第3天时硫化物的浓度降为4 mg/L.从第3天起所排污水中硫化物的浓度y与时间x满足下面表格中的关系:
时间x(天) | 3 | 4 | 5 | 6 | 8 | …… |
硫化物的浓y(mg/L) | 4 | 3 | 2.4 | 2 | 1.5 |
(1)求整改过程中当0≤x<3时,硫化物的浓度y与时间x的函数表达式;
(2)求整改过程中当x≥3时,硫化物的浓度y与时间x的函数表达式;
(3)该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的1.0 mg/L?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com