
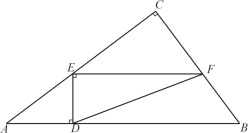
【题目】如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,D为AB边上的动点,过点D作DE⊥AB交边AC于点E,过点E作EF⊥DE交BC于点F,连接DF.
(1)当AD=4时,求EF的长度;
(2)求△DEF的面积的最大值;
(3)设O为DF的中点,随着点D的运动,则点O的运动路径的长度为______.
【答案】(1)![]() ,(2)6,(3)
,(2)6,(3)![]()
【解析】
(1)利用勾股定理可求出AB的长,根据∠A=∠A,∠EDA=∠C=90°可证明△AED∽△ABC,即可求出AE、CE的长,由∠EDA=∠DEF=90°可得EF//AB,即可证明△CEF∽△ACB,根据相似三角形的性质即可求出EF的长;(2)设AD=x.由△AED∽△ABC可得![]() =
=![]() =
=![]() ,即可用x表示出DE、AE的长,进而可表示CE的长,由△CEF∽△ACB可得
,即可用x表示出DE、AE的长,进而可表示CE的长,由△CEF∽△ACB可得![]() =
=![]() ,即可用x表示出EF的长,进而可用x表示出△DEF的面积,根据二次函数的性质即可求出△DEF的面积的最大值;(3)过C作CG⊥AB于G,当点D与A点重合时,点O为AB中点,当点D与点G重合时,点O为CG的中点,当点D在点G右边时,DE与AC无交点,点O不存在,设AB中点为O1,CG的中点为O2,根据△ABC的面积可求出CG的长,即可得O2G的长,利用勾股定理可求出BG的长,即可得O1G的长,利用勾股定理求出O1O2的长即可.
,即可用x表示出EF的长,进而可用x表示出△DEF的面积,根据二次函数的性质即可求出△DEF的面积的最大值;(3)过C作CG⊥AB于G,当点D与A点重合时,点O为AB中点,当点D与点G重合时,点O为CG的中点,当点D在点G右边时,DE与AC无交点,点O不存在,设AB中点为O1,CG的中点为O2,根据△ABC的面积可求出CG的长,即可得O2G的长,利用勾股定理可求出BG的长,即可得O1G的长,利用勾股定理求出O1O2的长即可.
(1)∵在Rt△ABC中,∠C=90°,
∴AB=![]() =
=![]() =10.
=10.
∵DE⊥AB,
∴∠EDA=90°.
∵∠A=∠A,∠EDA=∠C=90°,
∴△AED∽△ABC,
∴![]() =
=![]() .
.
∴AE=![]() AB=5.
AB=5.
∴CE=AC-AE=8-5=3.
∵DE⊥AB,
∴∠DEF=90°.
∵∠EDA=∠DEF=90°,
∴EF∥AB.
∴△CEF∽△ACB,
∴![]() =
=![]() .
.
∴EF=![]() ·AB=
·AB=![]() .
.
(2)解:设AD=x.
∵△AED∽△ABC,
∴![]() =
=![]() =
=![]() .
.
∴DE=![]() ·BC=
·BC=![]() x,AE=
x,AE=![]() ·AB=
·AB=![]() x.
x.
∴CE=AC-AE=8-![]() x.
x.
∵△CEF∽△ACB,
∴![]() =
=![]() .
.
∴EF=![]() ·AB=10-
·AB=10-![]() x.
x.
∴S△DEF=![]() DE·EF=-
DE·EF=-![]() x2+
x2+![]() x=-
x=-![]() (x-
(x-![]() )2+6.
)2+6.
∴当x=![]() 时,S△DEF取最大值为6.
时,S△DEF取最大值为6.
因此,△DEF的面积的最大值为6.
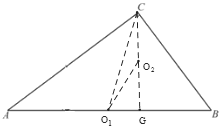
(3)过C作CG⊥AB于G,
当点D与A点重合时,点O为AB中点,当点D与点G重合时,点O为CG的中点,当点D在点G右边时,DE与AC无交点,点O不存在,设AB中点为O1,CG的中点为O2,
∴O1O2为点O的运动路径的长度,
∵S△ABC=![]() AC
AC![]() BC=
BC=![]() AB
AB![]() CG,
CG,
∴CG=![]() =
=![]() =
=![]() ,
,
∴O2G=![]() CG=
CG=![]() ,BG=
,BG=![]() =
=![]() ,
,
∵AB=10,
∴O1B=5,
∴O1G= O1B-BG=![]() ,
,
∴O1O2=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
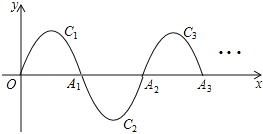
【题目】如图,在平面直角坐标系xOy中,已知抛物线y=﹣x(x﹣3)(0≤x≤3)在x轴上方的部分,记作C1,它与x轴交于点O,A1,将C1绕点A1旋转180°得C2,C2与x轴交于另一点A2.请继续操作并探究:将C2绕点A2旋转180°得C3,与x轴交于另一点A3;将C3绕点A3旋转180°得C4,与x轴交于另一点A4,这样依次得到x轴上的点A1,A2,A3,…,An,…,及抛物线C1,C2,…,n,…则n的顶点坐标为_____(n为正整数,用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=5,E是BC边上的一个动点,DF⊥AE,垂足为点F,连结CF
(1)若AE=BC
①求证:△ABE≌△DFA;②求四边形CDFE的周长;③求tan∠FCE的值;
(2)探究:当BE为何值时,△CDF是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某景区每日利润y1(元)与当天游客人数x(人)的函数图像.为了吸引游客,该景区决定改革,改革后每张票价减少20元,运营成本减少800元.设改革后该景区每日利润为y2(元).(注:每日利润=票价收入-运营成本)
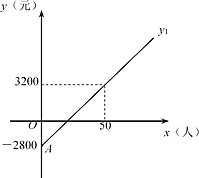
(1)解释点A的实际意义:______.
(2)分别求出y1、y2关于x的函数表达式;
(3)当游客人数为多少人时,改革前的日利润与改革后的日利润相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,飞机在一定高度上沿水平直线飞行,先在点![]() 处测得正前方小岛
处测得正前方小岛![]() 的俯角为
的俯角为![]() ,面向小岛方向继续飞行
,面向小岛方向继续飞行![]()
![]() 到达
到达![]() 处,发现小岛在其正后方,此时测得小岛的俯角为
处,发现小岛在其正后方,此时测得小岛的俯角为![]() .如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
.如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=2x+2与x轴,y轴分别交于点A,B,抛物线y=ax2+bx-![]() 经过点A和点C(4,0).
经过点A和点C(4,0).
(1)求该抛物线的表达式.
(2)连接CB,并延长CB至点D,使DB=CB,请判断点D是否在该抛物线上,并说明理由.
(3)在(2)的条件下,过点C作x轴的垂线EC与直线y=2x+2交于点E,以DE为直径画⊙M,
①求圆心M的坐标;②若直线AP与⊙M相切,P为切点,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF,若AB=2![]() ,∠DCF=30°,则EF的长为( )
,∠DCF=30°,则EF的长为( )

A. 4B. 6C. ![]() D. 2
D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com