
【题目】在平面直角坐标系xOy中,直线y=2x+2与x轴,y轴分别交于点A,B,抛物线y=ax2+bx-![]() 经过点A和点C(4,0).
经过点A和点C(4,0).
(1)求该抛物线的表达式.
(2)连接CB,并延长CB至点D,使DB=CB,请判断点D是否在该抛物线上,并说明理由.
(3)在(2)的条件下,过点C作x轴的垂线EC与直线y=2x+2交于点E,以DE为直径画⊙M,
①求圆心M的坐标;②若直线AP与⊙M相切,P为切点,直接写出点P的坐标.
【答案】(1)![]() ;(2)在,理由见试题解析;(3)①M(0,7);②P(-4,4)或P(3,3).
;(2)在,理由见试题解析;(3)①M(0,7);②P(-4,4)或P(3,3).
【解析】
试题(1)求出A、B的坐标,然后代入抛物线的解析式即可;
(2)过点D作DF垂直x轴于点F,由△CDF∽△CBO得到D的坐标,代入抛物线进行检验;
(3)①先求出E的坐标,设DE与y轴的交点为M′,证明M′就是圆心M,得出M的坐标;
②设P(x,y),则直线PA⊥MA,且MA=5,因为两条直线垂直,它们的k相乘为-1以及两点间距离公式,得到方程组,解方程组即可得到P的坐标.
试题解析:(1)依题意,可知 A(-1, 0),B(0,2),抛物线![]() 经过点A,C (4,0)所以有
经过点A,C (4,0)所以有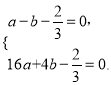 ,解得
,解得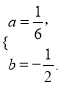 ,∴
,∴![]() ;
;
(2)点D在该抛物线上.依题意,可得BO=2,CO=4.过点D作DF垂直x轴于点F,∴△CDF∽△CBO,∴![]() ,∴DF=4,OF= CF-OC =4,∴ D(-4,4).∵
,∴DF=4,OF= CF-OC =4,∴ D(-4,4).∵![]() ,∴点D在该抛物线上;
,∴点D在该抛物线上;
(3)①由题意可知E(4,10),设DE与y轴的交点为M′,∵M′B∥EC,∴![]() ,∴D M′=EM′,∴M′ 即⊙M的圆心M,∴
,∴D M′=EM′,∴M′ 即⊙M的圆心M,∴![]() ,∴M(0,7).
,∴M(0,7).
②设P(x,y),则直线PA⊥MA,且MA=5,∵直线PA⊥MA,∴ ,解得:
,解得:![]() ,
,![]() ,∴P(-4,4)或P(3,3).
,∴P(-4,4)或P(3,3).



 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
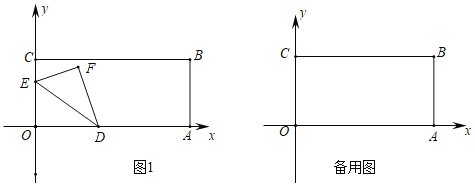
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A在x轴上,点C在y轴上,点B的坐标为(8,4),动点D从点O向点A以每秒两个单位的速度运动,动点E从点C向点O以每秒一个单位的速度运动,设D、E两点同时出发,运动时间为t秒,将△ODE沿DE翻折得到△FDE.
(1)若四边形ODFE为正方形,求t的值;
(2)若t=2,试证明A、F、C三点在同一直线上;
(3)是否存在实数t,使△BDE的面积最小?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
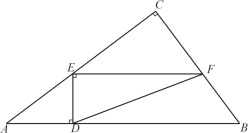
【题目】如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,D为AB边上的动点,过点D作DE⊥AB交边AC于点E,过点E作EF⊥DE交BC于点F,连接DF.
(1)当AD=4时,求EF的长度;
(2)求△DEF的面积的最大值;
(3)设O为DF的中点,随着点D的运动,则点O的运动路径的长度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图山坡上有一根旗杆AB,旗杆底部B点到山脚C点的距离BC为![]() 米,斜坡BC的坡度i=1:
米,斜坡BC的坡度i=1: ![]() .小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.
.小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.
(1)求坡角∠BCD;
(2)求旗杆AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)

查看答案和解析>>
科目:初中数学 来源: 题型:
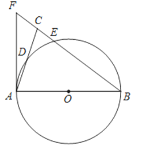
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE,AF的长.
,CE:EB=1:4,求CE,AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
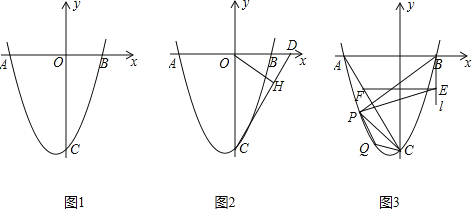
【题目】如图1,抛物线![]() 交x轴于点
交x轴于点![]() ,
,![]() ,交y轴于点C.
,交y轴于点C.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 如图2,D点坐标为
如图2,D点坐标为![]() ,连结
,连结![]() 若点H是线段DC上的一个动点,求
若点H是线段DC上的一个动点,求![]() 的最小值.
的最小值.
![]() 如图3,连结AC,过点B作x轴的垂线l,在第三象限中的抛物线上取点P,过点P作直线AC的垂线交直线l于点E,过点E作x轴的平行线交AC于点F,已知
如图3,连结AC,过点B作x轴的垂线l,在第三象限中的抛物线上取点P,过点P作直线AC的垂线交直线l于点E,过点E作x轴的平行线交AC于点F,已知![]() .
.
![]() 求点P的坐标;
求点P的坐标;
![]() 在抛物线
在抛物线![]() 上是否存在一点Q,使得
上是否存在一点Q,使得![]() 成立?若存在,求出Q点坐标;若不存在,请说明理由.
成立?若存在,求出Q点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣6x+k+3=0有两个不相等的实数根
(1)求k的取值范围;
(2)若k为大于3的整数,且该方程的根都是整数,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= °;
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
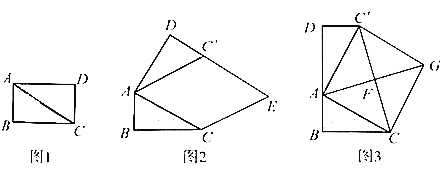
【题目】问题情填,
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动,如图1,将矩形纸片ABCD沿对角线AC剪开,得到△ABC和△ACD、并且量得AB=2cm,AC=4cm.
操作发现:
(1)将图1中的△ACD以点A为旋转中心,按逆时针方向旋转∠α,使∠α=∠BAC,得到加图2所示的△AC′D,过点C作AC′的平行线,与DC′的延长线交于点E,则四边形ACEC'的形状是_________;
(2)创新小组将图1中的△ACD以点A为旋转中心,按逆时针方向旋转,使B,A,D三点在同一条直线上,得到如图3所示的△AC′D,连接CC′,取CC'的中点F,连精AF并延长到点G,使FG=AF,连接CG,C′G,得到四边形ACGC′,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将△ABC沿着BD方向平移,使点B与点A重合,此时A点平移至A′点,A′C与BC′相交于点H.如图4所示,连接CC',试求CH的长度.
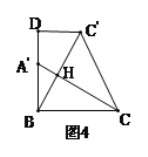
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com