
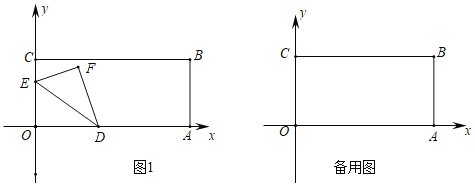
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ҫШРОOABCөД¶ҘөгAФЪxЦбЙПЈ¬өгCФЪyЦбЙПЈ¬өгBөДЧшұкОӘЈЁ8Ј¬4Ј©Ј¬¶ҜөгDҙУөгOПтөгAТФГҝГлБҪёцөҘО»өДЛЩ¶ИФЛ¶ҜЈ¬¶ҜөгEҙУөгCПтөгOТФГҝГлТ»ёцөҘО»өДЛЩ¶ИФЛ¶ҜЈ¬ЙиDЎўEБҪөгН¬Кұіц·ўЈ¬ФЛ¶ҜКұјдОӘtГлЈ¬Ҫ«ЎчODEСШDE·ӯХЫөГөҪЎчFDEЈ®
ЈЁ1Ј©ИфЛДұЯРОODFEОӘХэ·ҪРОЈ¬ЗуtөДЦөЈ»
ЈЁ2Ј©ИфtЈҪ2Ј¬КФЦӨГчAЎўFЎўCИэөгФЪН¬Т»ЦұПЯЙПЈ»
ЈЁ3Ј©КЗ·сҙжФЪКөКэtЈ¬К№ЎчBDEөДГж»эЧоРЎЈҝИфҙжФЪЈ¬ЗуіцtөДЦөЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©tЈҪ![]() Ј»ЈЁ2Ј©јыҪвОцЈ»ЈЁ3Ј©ҙжФЪКөКэtЈ¬К№ЎчBDEөДГж»эЧоРЎЈ¬tЈҪ2ГлЈ®АнУЙјыҪвОц.
Ј»ЈЁ2Ј©јыҪвОцЈ»ЈЁ3Ј©ҙжФЪКөКэtЈ¬К№ЎчBDEөДГж»эЧоРЎЈ¬tЈҪ2ГлЈ®АнУЙјыҪвОц.
ЎҫҪвОцЎҝ
ЈЁ1Ј©УЙХэ·ҪРОөДРФЦКөГіцOEЎОDFЈ¬OE=DFУЙХЫөюөДРФЦКөГіцOD=DFЈ¬УЙOD=2tЈ¬OE=4-tЈ¬өГіц·ҪіМ2t=4-tЈ¬Ҫв·ҪіМјҙҝЙЈ»
ЈЁ2Ј©Б¬ҪУACЈ¬ЧчOGЎНACУЪGЈ¬УЙt=2Ј¬өГіцOE=CE=2Ј¬OD=DA=4Ј¬УЙИэҪЗРОЦРО»ПЯ¶ЁАнөГіцDEЎОACЈ¬ЗТDE=![]() ACЈ¬УЙЖҪРРПЯөГіц
ACЈ¬УЙЖҪРРПЯөГіц![]() Ј¬өГіцDEҙ№ЦұЖҪ·ЦOFЈ¬өГіцGУлFөгЦШәПЈ¬јҙҝЙөГіцҪбВЫЈ»
Ј¬өГіцDEҙ№ЦұЖҪ·ЦOFЈ¬өГіцGУлFөгЦШәПЈ¬јҙҝЙөГіцҪбВЫЈ»
ЈЁ3Ј©УЙМвТвөГіцSЎчBDE=SҫШРОOABC-SЎчBCE-SЎчABD-SЎчODE=t2-4t+16Ј¬УЙ¶юҙОәҜКэөДРФЦКјҙҝЙөГіцҪб№ыЈ®
ЈЁ1Ј©ҪвЈәЎЯҫШРОOABCЦРЈ¬BЈЁ8Ј¬4Ј©Ј¬
ЎаOAЈҪ8Ј¬OCЈҪ4Ј¬
ЎЯЛДұЯРОODEFОӘХэ·ҪРОЈ¬
ЎаOEЎОDFЈ¬OEЈҪDFЈ¬
ЎЯЎчODEСШDE·ӯХЫөГөҪЎчFDEЈ¬
ЎаODЈҪDFЈ¬
ЎЯODЈҪ2tЈ¬OEЈҪ4©ҒtЈ¬
Ўа2tЈҪ4©ҒtЈ¬tЈҪ![]() Ј»
Ј»
ЈЁ2Ј©ЦӨГчЈәБ¬ҪУACЈ¬ЧчOGЎНACУЪGЈ¬ИзНј1ЛщКҫЈә
ЎЯtЈҪ2Ј¬
ЎаOEЈҪBEЈҪ2Ј¬ODЈҪDEЈҪ4Ј¬
ЎаDEКЗЎчOACөДЦРО»ПЯЈ¬
ЎаDEЎОACЈ¬ЗТDEЈҪ![]() ACЈ¬
ACЈ¬
Ўа![]()
ЎаDEҙ№ЦұЖҪ·ЦOFЈ¬
УЙХЫөюөДРФЦКөГЈәDEҙ№ЦұЖҪ·ЦOFЈ¬
ЎаGУлFөгЦШәПЈ¬
јҙAЎўCЎўFИэөгФЪН¬Т»МхЦұПЯЈ»
ЈЁ3Ј©ҪвЈәҙжФЪЈ¬АнУЙИзПВЈәИзНј2ЛщКҫЈә
ЎЯSЎчBDEЈҪSЎчABC©ҒSЎчBCE©ҒSЎчABD©ҒSЎчODE
ЈҪ![]()
ЈҪ32©Ғ4t©Ғ16+4t©Ғ4t+t2
ЈҪt2©Ғ4t+16
ЈҪЈЁt©Ғ2Ј©2+12Ј¬
ЎаtЈҪ2КұЈ¬SЎчBDEУРЧоРЎЦөОӘ12Ј»
јҙҙжФЪКөКэtЈ¬К№ЎчBDEөДГж»эЧоРЎЈ¬tЈҪ2ГлЈ®


 УЕ°Щ·ЦҝОКұ»Ҙ¶ҜПөБРҙр°ё
УЕ°Щ·ЦҝОКұ»Ҙ¶ҜПөБРҙр°ё ҝӘРДНЬЧҙФӘЧчТөПөБРҙр°ё
ҝӘРДНЬЧҙФӘЧчТөПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЛДұЯРО![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬¶Ҝөг
Ј¬¶Ҝөг![]() Ј¬
Ј¬![]() Н¬КұҙУөг
Н¬КұҙУөг![]() іц·ўЈ¬өг
іц·ўЈ¬өг![]() ТФ
ТФ![]() өДЛЩ¶ИСШХЫПЯ
өДЛЩ¶ИСШХЫПЯ![]() ФЛ¶ҜөҪөг
ФЛ¶ҜөҪөг![]() Ј¬өг
Ј¬өг![]() ТФ
ТФ![]() өДЛЩ¶ИСШ
өДЛЩ¶ИСШ![]() ФЛ¶ҜөҪөг
ФЛ¶ҜөҪөг![]() Ј¬Йи
Ј¬Йи![]() Ј¬
Ј¬![]() Н¬Кұіц·ў
Н¬Кұіц·ў![]() КұЈ¬
КұЈ¬![]() өДГж»эОӘ
өДГж»эОӘ![]() Ј¬Фт
Ј¬Фт![]() Ул
Ул![]() өДәҜКэНјПуҙуЦВКЗ( )
өДәҜКэНјПуҙуЦВКЗ( )
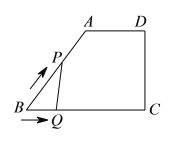
A. 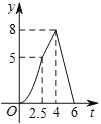 B.
B. 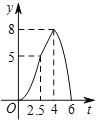
C. 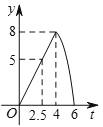 D.
D. 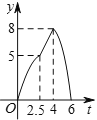
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘ¶юҙОәҜКэ![]() өДНјПуИзНјЛщКҫЈ¬ПВБРҪбВЫЈә
өДНјПуИзНјЛщКҫЈ¬ПВБРҪбВЫЈә
ўЩ![]() Ј»ўЪ
Ј»ўЪ![]() Ј»ўЫ
Ј»ўЫ![]() Ј»ўЬ
Ј»ўЬ![]() Ј»ўЭ
Ј»ўЭ![]() Ј»ўЮөұ
Ј»ўЮөұ![]() КұЈ¬
КұЈ¬![]() Лж
Лж![]() өДФцҙу¶шФцҙуЈ®
өДФцҙу¶шФцҙуЈ®
ЖдЦРХэИ·өДЛө·ЁУР________ЈЁРҙіцХэИ·Лө·ЁөДРтәЕЈ©

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОӘ·бё»С§ЙъөДҝОУаЙъ»оЈ¬С§РЈЧјұё№әВтІҝ·ЦМеУэЖчІДЈ¬ТФВъЧгС§ЙъГЗөДРиЗуЈ®С§РЈ¶ФЎ°ОТЧоПІ°®өДМеУэФЛ¶ҜЎұҪшРРБЛійСщөчІйЈЁГҝёцС§ЙъЦ»СЎТ»ҙОЈ©Ј¬ёщҫЭөчІйҪб№ы»жіЙИзНјЛщКҫөДБҪ·щІ»НкХыНіјЖНјЈ¬ЗлДгёщҫЭНіјЖНјМṩөДРЕПўҪвҙрПВБРОКМвЈ®
ЈЁ1Ј©ЗуmЎўnөДЦөЈ»
ЈЁ2Ј©ИфёГРЈУР2000ГыС§ЙъЈ¬ЗлДгёщҫЭСщұҫКэҫЭЈ¬№АЛгёГРЈПІ»¶МЯЧгЗтөДС§ЙъИЛКэКЗ¶аЙЩЈҝ
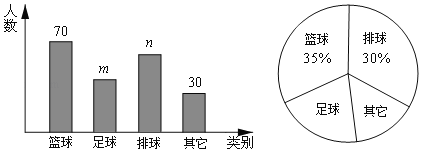
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЛщКҫЈ¬ФЪҫШРО![]() ЦРЈ¬ТСЦӘ
ЦРЈ¬ТСЦӘ![]() Ј¬
Ј¬![]() Ј¬өг
Ј¬өг![]() СШ
СШ![]() ұЯҙУөг
ұЯҙУөг![]() ҝӘКјПтөг
ҝӘКјПтөг![]() ТФГҝГл
ТФГҝГл![]() ёцөҘО»іӨ¶ИөДЛЩ¶ИФЛ¶ҜЈ»өг
ёцөҘО»іӨ¶ИөДЛЩ¶ИФЛ¶ҜЈ»өг![]() СШ
СШ![]() ұЯҙУөг
ұЯҙУөг![]() ҝӘКјПтөг
ҝӘКјПтөг![]() ТФГҝГл
ТФГҝГл![]() ёцөҘО»іӨ¶ИөДЛЩ¶ИФЛ¶ҜЈ®Из№ы
ёцөҘО»іӨ¶ИөДЛЩ¶ИФЛ¶ҜЈ®Из№ы![]() Ј¬
Ј¬![]() Н¬Кұіц·ўЈ¬УГ
Н¬Кұіц·ўЈ¬УГ![]() ГлұнКҫФЛ¶ҜөДКұјдЈ®
ГлұнКҫФЛ¶ҜөДКұјдЈ®

ЗлҪвҙрПВБРОКМвЈә
ЈЁ1Ј©өұ![]() ОӘәОЦөКұЈ¬
ОӘәОЦөКұЈ¬![]() КЗөИСьЦұҪЗИэҪЗРОЈҝ
КЗөИСьЦұҪЗИэҪЗРОЈҝ
ЈЁ2Ј©өұ![]() tОӘәОЦөКұЈ¬ТФөг
tОӘәОЦөКұЈ¬ТФөг![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ОӘ¶ҘөгөДИэҪЗРОУл
ОӘ¶ҘөгөДИэҪЗРОУл![]() ПаЛЖЈҝ
ПаЛЖЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬ТСЦӘЕЧОпПЯyЈҪ©ҒxЈЁx©Ғ3Ј©ЈЁ0ЎЬxЎЬ3Ј©ФЪxЦбЙП·ҪөДІҝ·ЦЈ¬јЗЧчC1Ј¬ЛьУлxЦбҪ»УЪөгOЈ¬A1Ј¬Ҫ«C1ИЖөгA1РэЧӘ180ЎгөГC2Ј¬C2УлxЦбҪ»УЪБнТ»өгA2Ј®ЗлјМРшІЩЧчІўМҪҫҝЈәҪ«C2ИЖөгA2РэЧӘ180ЎгөГC3Ј¬УлxЦбҪ»УЪБнТ»өгA3Ј»Ҫ«C3ИЖөгA3РэЧӘ180ЎгөГC4Ј¬УлxЦбҪ»УЪБнТ»өгA4Ј¬ХвСщТАҙОөГөҪxЦбЙПөДөгA1Ј¬A2Ј¬A3Ј¬ЎӯЈ¬AnЈ¬ЎӯЈ¬ј°ЕЧОпПЯC1Ј¬C2Ј¬ЎӯЈ¬nЈ¬ЎӯФтnөД¶ҘөгЧшұкОӘ_____ЈЁnОӘХэХыКэЈ¬УГә¬nөДҙъКэКҪұнКҫЈ©Ј®
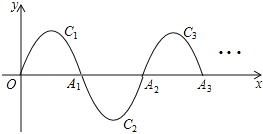
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪҫШРОABCDЦРЈ¬ABЈҪ4Ј¬BCЈҪ5Ј¬EКЗBCұЯЙПөДТ»ёц¶ҜөгЈ¬DFЎНAEЈ¬ҙ№ЧгОӘөгFЈ¬Б¬ҪбCF
ЈЁ1Ј©ИфAEЈҪBC
ўЩЗуЦӨЈәЎчABEЎХЎчDFAЈ»ўЪЗуЛДұЯРОCDFEөДЦЬіӨЈ»ўЫЗуtanЎПFCEөДЦөЈ»
ЈЁ2Ј©МҪҫҝЈәөұBEОӘәОЦөКұЈ¬ЎчCDFКЗөИСьИэҪЗРОЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬ЦұПЯyЈҪ2xЈ«2УлxЦбЈ¬yЦб·ЦұрҪ»УЪөгAЈ¬BЈ¬ЕЧОпПЯy=ax2Ј«bxЈӯ![]() ҫӯ№эөгAәНөгC(4,0)Ј®
ҫӯ№эөгAәНөгC(4,0)Ј®
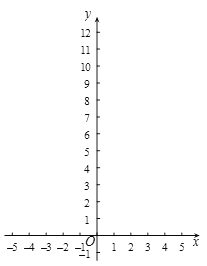
ЈЁ1Ј©ЗуёГЕЧОпПЯөДұнҙпКҪЈ®
ЈЁ2Ј©Б¬ҪУCBЈ¬ІўСУіӨCBЦБөгDЈ¬К№DB=CBЈ¬ЗлЕР¶ПөгDКЗ·сФЪёГЕЧОпПЯЙПЈ¬ІўЛөГчАнУЙЈ®
ЈЁ3Ј©ФЪЈЁ2Ј©өДМхјюПВЈ¬№эөгCЧчxЦбөДҙ№ПЯECУлЦұПЯyЈҪ2xЈ«2Ҫ»УЪөгEЈ¬ТФDEОӘЦұҫ¶»ӯЎСMЈ¬
ўЩЗуФІРДMөДЧшұкЈ»ўЪИфЦұПЯAPУлЎСMПаЗРЈ¬PОӘЗРөгЈ¬ЦұҪУРҙіцөгPөДЧшұкЈ®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com