
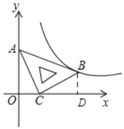
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )

A. (![]() ,0) B. (2,0) C. (
,0) B. (2,0) C. (![]() ,0) D. (3,0)
,0) D. (3,0)
【答案】A
【解析】分析:过点B作BD⊥x轴于点D,易证△ACO≌△BCD(AAS),从而可求出B的坐标,进而可求出反比例函数的解析式,根据解析式与A的坐标即可得知平移的单位长度,从而求出C的对应点.
详解:
过点B作BD⊥x轴于点D,如图所示:
∵∠ACO+∠BCD=90°,
∠OAC+∠ACO=90°,
∴∠OAC=∠BCD,
在△ACO与△BCD中,
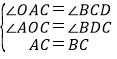
∴△ACO≌△BCD(AAS)
∴OC=BD,OA=CD,
∵A(0,2),C(1,0)
∴OD=3,BD=1,
∴B(3,1),
∴设反比例函数的解析式为y=![]() ,
,
将B(3,1)代入y=![]() ,
,
∴k=3,
∴y=![]() ,
,
∴把y=2代入y=![]() ,
,
∴x=![]() ,
,
当顶点A恰好落在该双曲线上时,
此时点A移动了![]() 个单位长度,
个单位长度,
∴C也移动了![]() 个单位长度,
个单位长度,
此时点C的对应点C′的坐标为(![]() ,0)
,0)
故选:A.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】在某电视台的一档选秀节目中,有三位评委,每位评委在选手完成才艺表演后,出示“通过”(用√表示)或“淘汰”(用×表示)的评定结果,节目组规定:每位选手至少获得两位评委的“通过”才能晋级.
(1)请用树状图列举出选手A获得三位评委评定的各种可能的结果;
(2)求选手A晋级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以每秒
以每秒![]() 个单位长度的速度运动;点
个单位长度的速度运动;点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以每秒
以每秒![]() 个单位长度的速度运动.如果
个单位长度的速度运动.如果![]() ,
,![]() 同时出发,用
同时出发,用![]() 秒表示运动的时间.
秒表示运动的时间.

请解答下列问题:
(1)当![]() 为何值时,
为何值时,![]() 是等腰直角三角形?
是等腰直角三角形?
(2)当![]() t为何值时,以点
t为何值时,以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知抛物线y=﹣x(x﹣3)(0≤x≤3)在x轴上方的部分,记作C1,它与x轴交于点O,A1,将C1绕点A1旋转180°得C2,C2与x轴交于另一点A2.请继续操作并探究:将C2绕点A2旋转180°得C3,与x轴交于另一点A3;将C3绕点A3旋转180°得C4,与x轴交于另一点A4,这样依次得到x轴上的点A1,A2,A3,…,An,…,及抛物线C1,C2,…,n,…则n的顶点坐标为_____(n为正整数,用含n的代数式表示).
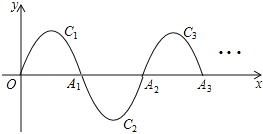
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了改善办公条件,计划从厂家购买![]() 两种型号电脑.已知每台
两种型号电脑.已知每台![]() 种型号电脑价格比每台
种型号电脑价格比每台![]() 种型号电脑价格多0.1万元,且用10万元购买
种型号电脑价格多0.1万元,且用10万元购买![]() 种型号电脑的数量与用8万购买
种型号电脑的数量与用8万购买![]() 种型号电脑的数量相同.
种型号电脑的数量相同.
(1)求![]() 两种型号电脑每台价格各为多少万元?
两种型号电脑每台价格各为多少万元?
(2)学校预计用不多于9.2万元的资金购进这两种电脑共20台,其中![]() 种型号电脑至少要购进10台,请问有哪几种购买方案?
种型号电脑至少要购进10台,请问有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=5,E是BC边上的一个动点,DF⊥AE,垂足为点F,连结CF
(1)若AE=BC
①求证:△ABE≌△DFA;②求四边形CDFE的周长;③求tan∠FCE的值;
(2)探究:当BE为何值时,△CDF是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某景区每日利润y1(元)与当天游客人数x(人)的函数图像.为了吸引游客,该景区决定改革,改革后每张票价减少20元,运营成本减少800元.设改革后该景区每日利润为y2(元).(注:每日利润=票价收入-运营成本)
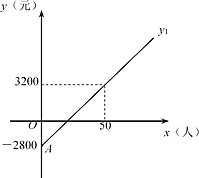
(1)解释点A的实际意义:______.
(2)分别求出y1、y2关于x的函数表达式;
(3)当游客人数为多少人时,改革前的日利润与改革后的日利润相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自我省深化课程改革以来,某校开设了:A.利用影长求物体高度,B.制作视力表,C.设计遮阳棚,D.制作中心对称图形,四类数学实践活动课.规定每名学生必选且只能选修一类实践活动课,学校对学生选修实践活动课的情况进行抽样调查,将调查结果绘制成如下两幅不完整的统计图.
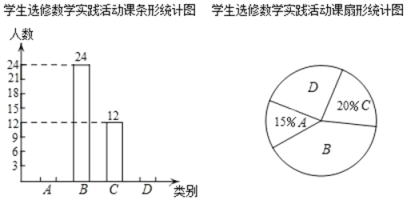
根据图中信息解决下列问题:
(1)本次共调查名学生,扇形统计图中B所对应的扇形的圆心角为度;
(2)补全条形统计图;
(3)选修D类数学实践活动的学生中有2名女生和2名男生表现出色,现从4人中随机抽取2人做校报设计,请用列表或画树状图法求所抽取的两人恰好是1名女生和1名男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com