
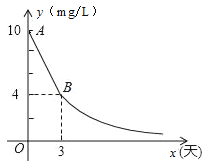
【题目】环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0 mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,其中第3天时硫化物的浓度降为4 mg/L.从第3天起所排污水中硫化物的浓度y与时间x满足下面表格中的关系:
时间x(天) | 3 | 4 | 5 | 6 | 8 | …… |
硫化物的浓y(mg/L) | 4 | 3 | 2.4 | 2 | 1.5 |
(1)求整改过程中当0≤x<3时,硫化物的浓度y与时间x的函数表达式;
(2)求整改过程中当x≥3时,硫化物的浓度y与时间x的函数表达式;
(3)该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的1.0 mg/L?为什么?
【答案】(1) y=-![]() x+15;(2) y=
x+15;(2) y=![]() ;(3)该企业所排污水中硫化物的浓度,能在15天以内不超过最高允许的1.0mg/L,理由详见解析.
;(3)该企业所排污水中硫化物的浓度,能在15天以内不超过最高允许的1.0mg/L,理由详见解析.
【解析】
(1)设线段AB的函数表达式为:y=kx+b,把A、B两点坐标代入求出k、b的值即可.(2)设函数的表达式为:y=![]() ,把B点坐标代入,求出k的值即可.(3)根据(2)所得表达式,求出x=15时,y的值与硫化物浓度允许的最高值比较即可.
,把B点坐标代入,求出k的值即可.(3)根据(2)所得表达式,求出x=15时,y的值与硫化物浓度允许的最高值比较即可.
(1)前三天的函数图象是线段,设函数表达式为:y=kx+b
把(0,15)(3,4)代入函数关系式,得![]()
解得:k=﹣![]() ,b=15
,b=15
所以当0≤x<3时,硫化物的浓度y与时间x的函数表达式为:y=﹣![]() x+15;
x+15;
(2)当x≥3时,设y=![]()
把(3,4)代入函数表达式,得4=![]()
所以k=12
当x≥3时,硫化物的浓度y与时间x的函数表达式为:y=![]()
(3)能.理由:
当x=15时,y=![]() =0.8
=0.8
因为0.8<1,
所以该企业所排污水中硫化物的浓度,能在15天以内不超过最高允许的1.0mgL


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,BE交AD于点F,交AC于点E,若BE平分∠ABC,试判断△AEF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用直尺和圆规作一个角∠A′O′B′,等于已知角∠AOB,能得出∠A′O′B′=∠AOB的依据是( )

A.SASB.ASAC.AASD.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“五一”劳动节期间,某商场为吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准标有数字的区域(未标数字的视为0),则顾客就可以分别获得该区域相应数字的返金券,凭返金券可以在该商场继续购物.若顾客不愿意转转盘,则每购物满200元可享受九五折优惠.
(1)写出转动一次转盘获得返金券的概率;
(2)转转盘和直接享受九五折优惠,你认为哪种方式对顾客更合算?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,D、E、F分别是AC、BC、AB的中点,连接DE.点P从点D出发,沿DE方向匀速运动;同时,点Q从点E出发,沿EB方向匀速运动,两者速度均为1cm/s;当其中一点停止运动时,另外一点也停止运动.连接PQ、PF,设运动时间为ts(0<t<4).解答下列问题:
(1)当t为何值时,△EPQ为等腰三角形?
(2)如图①,设四边形PFBQ的面积为ycm2,求y与t之间的函数关系式;
(3)当t为何值时,四边形PFBQ的面积与△ABC的面积之比为2:5?
(4)如图②,连接FQ,是否存在某一时刻,使得PF与QF互相垂直?若存在,求出此时t的值;若不存,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款![]() 元,第三天收到捐款
元,第三天收到捐款![]() 元.
元.
![]() 如果第二天、第三天收到捐款的增长率相同,求捐款增长率?
如果第二天、第三天收到捐款的增长率相同,求捐款增长率?
![]() 按照
按照![]() 中收到捐款的增长率不变,该单位三天一共能收到多少捐款?
中收到捐款的增长率不变,该单位三天一共能收到多少捐款?
查看答案和解析>>
科目:初中数学 来源: 题型:
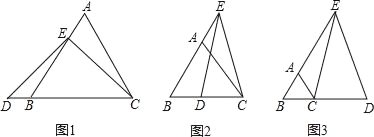
【题目】已知△ABC为等边三角形,E为射线BA上一点,D为直线BC上一点,ED=EC.
(1)当点E在AB的上,点D在CB的延长线上时(如图1),求证:AE+AC=CD;
(2)当点E在BA的延长线上,点D在BC上时(如图2),猜想AE、AC和CD的数量关系,并证明你的猜想;
(3)当点E在BA的延长线上,点D在BC的延长线上时(如图3),请直接写出AE、AC和CD的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com