
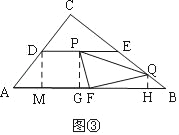
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌAC=6cmЃЌBC=8cmЃЌDЁЂEЁЂFЗжБ№ЪЧACЁЂBCЁЂABЕФжаЕуЃЌСЌНгDEЃЎЕуPДгЕуDГіЗЂЃЌбиDEЗНЯђдШЫйдЫЖЏЃЛЭЌЪБЃЌЕуQДгЕуEГіЗЂЃЌбиEBЗНЯђдШЫйдЫЖЏЃЌСНепЫйЖШОљЮЊ1cm/sЃЛЕБЦфжавЛЕуЭЃжЙдЫЖЏЪБЃЌСэЭтвЛЕувВЭЃжЙдЫЖЏЃЎСЌНгPQЁЂPFЃЌЩшдЫЖЏЪБМфЮЊtsЃЈ0ЃМtЃМ4ЃЉЃЎНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЕБtЮЊКЮжЕЪБЃЌЁїEPQЮЊЕШбќШ§НЧаЮЃП
ЃЈ2ЃЉШчЭМЂйЃЌЩшЫФБпаЮPFBQЕФУцЛ§ЮЊycm2ЃЌЧѓyгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЕБtЮЊКЮжЕЪБЃЌЫФБпаЮPFBQЕФУцЛ§гыЁїABCЕФУцЛ§жЎБШЮЊ2ЃК5ЃП
ЃЈ4ЃЉШчЭМЂкЃЌСЌНгFQЃЌЪЧЗёДцдкФГвЛЪБПЬЃЌЪЙЕУPFгыQFЛЅЯрДЙжБЃПШєДцдкЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉЕБt=![]() ЪБЃЌЁїEPQЮЊЕШбќШ§НЧаЮЃЛЃЈ2ЃЉy=
ЪБЃЌЁїEPQЮЊЕШбќШ§НЧаЮЃЛЃЈ2ЃЉy=![]() ЃЛЃЈ3ЃЉ1ЃЛЃЈ4ЃЉt=
ЃЛЃЈ3ЃЉ1ЃЛЃЈ4ЃЉt=![]() ЪБЃЌPFгыQFЛЅЯрДЙжБ.
ЪБЃЌPFгыQFЛЅЯрДЙжБ.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЙДЙЩЖЈРэЧѓГіAB=10ЃЌгЩDEЪЧжаЮЛЯпПЩжЊDE=5ЃЌЁїEPQЮЊЕШбќШ§НЧаЮжЛашPE=EQЃЌМДt=5-t,НтЗНГЬМДПЩ.ЃЈ2ЃЉЙ§PзїPHЁЭBCгкHЃЌСЌНгFEЃЌгЩsinЁЯPEH=![]() ЃЌПЩжЊPH=
ЃЌПЩжЊPH=![]() ЃЌМДЁїEQPЕФИпЃЌИљОнЁїCDEПЩЧѓГіDEБпЕФИпЃЌМДЁїPEFКЭЁїEFBЕФИпЃЌИљОнy=SЁїPEF+SЁїEFBЉSЁїEQPЃЌМДПЩЕУД№АИЃЛЃЈ3ЃЉЯШЧѓГіЁїABCЕФУцЛ§ЃЌИљОнЃЈ2ЃЉЫљЕУЙиЯЕЪНМАвбжЊУцЛ§БШЃЌСаЗНГЬМДПЩЕУД№АИ.ЃЈ4ЃЉШчЭМЂлЙ§PзїPGЁЭABгкGЃЌЙ§QзїQHЁЭABгкHЃЌЙ§DзїDMЁЭABгкMЃЌгЩЙДЙЩЖЈРэПЩжЊAMЕФГЄЃЌЁїBHQжаЃЌРћгУЁЯBЕФШ§НЧКЏЪ§жЕПЩЕУBHЁЂQHЕФГЄЃЌгЩPFЁЭFQЃЌПЩжЄУїЁїPGFЁзЁїFHQЃЌИљОнЖдгІБпЕФЙиЯЕСаГіЗНГЬМДПЩЧѓЕУtЕФжЕ.
ЃЌМДЁїEQPЕФИпЃЌИљОнЁїCDEПЩЧѓГіDEБпЕФИпЃЌМДЁїPEFКЭЁїEFBЕФИпЃЌИљОнy=SЁїPEF+SЁїEFBЉSЁїEQPЃЌМДПЩЕУД№АИЃЛЃЈ3ЃЉЯШЧѓГіЁїABCЕФУцЛ§ЃЌИљОнЃЈ2ЃЉЫљЕУЙиЯЕЪНМАвбжЊУцЛ§БШЃЌСаЗНГЬМДПЩЕУД№АИ.ЃЈ4ЃЉШчЭМЂлЙ§PзїPGЁЭABгкGЃЌЙ§QзїQHЁЭABгкHЃЌЙ§DзїDMЁЭABгкMЃЌгЩЙДЙЩЖЈРэПЩжЊAMЕФГЄЃЌЁїBHQжаЃЌРћгУЁЯBЕФШ§НЧКЏЪ§жЕПЩЕУBHЁЂQHЕФГЄЃЌгЩPFЁЭFQЃЌПЩжЄУїЁїPGFЁзЁїFHQЃЌИљОнЖдгІБпЕФЙиЯЕСаГіЗНГЬМДПЩЧѓЕУtЕФжЕ.
ЃЈ1ЃЉЁЯC=90ЁуЃЌAC=6cmЃЌBC=8cmЃЌ
ЁрAB=10cmЃЌ
гЩЬтвтЕУЃКDP=EQ=tЃЌ
ЁпDЮЊACЕФжаЕуЃЌEЮЊBCЕФжаЕуЃЌ
ЁрDE=![]() AB=5cmЃЌ
AB=5cmЃЌ
ЕБEP=EQЪБЃЌ5Љt=tЃЌ
t=![]() ЃЌ
ЃЌ
МДЕБt=![]() ЪБЃЌЁїEPQЮЊЕШбќШ§НЧаЮЃЛ
ЪБЃЌЁїEPQЮЊЕШбќШ§НЧаЮЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌЙ§PзїPHЁЭBCгкHЃЌСЌНгFEЃЌ
sinЁЯPEH=![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрPH=![]() ЃЌ
ЃЌ
ЩшЁїDCEжаЃЌDEБпЩЯЕФИпЮЊhЃЌ
![]() ЁС3ЁС4=
ЁС3ЁС4=![]() ЁС5hЃЌh=
ЁС5hЃЌh=![]() ЃЌ
ЃЌ
Ёрy=SЁїPEF+SЁїEFBЉSЁїEQPЃЌ
=![]() ЁС
ЁС![]() PE+
PE+![]() ЁС
ЁС![]() FBЉ
FBЉ![]() EQPHЃЌ
EQPHЃЌ
=![]() ЃЈ5ЉtЃЉ+
ЃЈ5ЉtЃЉ+![]() ЁС5Љ
ЁС5Љ![]() ЃЌ
ЃЌ
=![]() Љ
Љ![]() t+12ЃЛ
t+12ЃЛ
ЃЈ3ЃЉЁп![]() ЃЌ
ЃЌ
Ёр5SЫФБпаЮPFBQ=2SЁїABCЃЌ
Ёр5ЃЈ![]() Љ
Љ![]() t+12ЃЉ=2ЁС
t+12ЃЉ=2ЁС![]() ЁС6ЁС8ЃЌ
ЁС6ЁС8ЃЌ
t2Љ9t+8=0ЃЌ
t1=1ЃЌt2=8ЃЈЩсЃЉЃЛ
ЃЈ4ЃЉШчЭМЂлЃЌЙ§PзїPGЁЭABгкGЃЌЙ§QзїQHЁЭABгкHЃЌЙ§DзїDMЁЭABгкMЃЌ
гЩЃЈ3ЃЉжЊЃКPG=DM=![]() ЃЌ
ЃЌ
RtЁїADMжаЃЌЁпAD=3ЃЌ
ЁрAM=![]() ЃЌ
ЃЌ
ЁрFG=5Љ![]() Љt=
Љt=![]() ЉtЃЌ
ЉtЃЌ
RtЁїQHBжаЃЌBQ=4ЉtЃЌ
sinЁЯB=![]() ЃЌ
ЃЌ
ЁрQH=![]() ЃЌ
ЃЌ
ЁрBH=![]() ЃЌ
ЃЌ
ЁрFH=5ЉBH=![]() ЃЌ
ЃЌ
ЁпPFЁЭFQЃЌ
взЕУЁїPGFЁзЁїFHQЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрPGQH=FHGFЃЌ
Ёр![]() ЃЌ
ЃЌ
4t2Љ11t=0ЃЌ
t1=0ЃЈЩсЃЉЃЌt2=![]() ЃЎ
ЃЎ
ЁрЕБt=![]() ЪБЃЌPFгыQFЛЅЯрДЙжБЃЎ
ЪБЃЌPFгыQFЛЅЯрДЙжБЃЎ


 ЧЇРяТэзпЯђМйЦкЦкФЉЗТецЪдОэКЎМйЯЕСаД№АИ
ЧЇРяТэзпЯђМйЦкЦкФЉЗТецЪдОэКЎМйЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгквЛдЊЖўДЮЗНГЬ![]() ЃЌЯТСаЫЕЗЈЃК
ЃЌЯТСаЫЕЗЈЃК
ЂйШє![]() ЃЌЗНГЬ
ЃЌЗНГЬ![]() гаСНИіВЛЕШЕФЪЕЪ§ИљЃЛ
гаСНИіВЛЕШЕФЪЕЪ§ИљЃЛ
ЂкШєЗНГЬ![]() гаСНИіВЛЕШЕФЪЕЪ§ИљЃЌдђЗНГЬ
гаСНИіВЛЕШЕФЪЕЪ§ИљЃЌдђЗНГЬ![]() вВвЛЖЈгаСНИіВЛЕШЕФЪЕЪ§ИљЃЛ
вВвЛЖЈгаСНИіВЛЕШЕФЪЕЪ§ИљЃЛ
ЂлШє![]() ЪЧЗНГЬ
ЪЧЗНГЬ![]() ЕФвЛИіИљЃЌдђвЛЖЈга
ЕФвЛИіИљЃЌдђвЛЖЈга![]() ГЩСЂЃЛ
ГЩСЂЃЛ
ЂмШє![]() ЪЧЗНГЬ
ЪЧЗНГЬ![]() ЕФвЛИіИљЃЌдђвЛЖЈга
ЕФвЛИіИљЃЌдђвЛЖЈга![]() ГЩСЂЃЌЦфжае§ШЗЕФжЛгаЃЈ ЃЉ
ГЩСЂЃЌЦфжае§ШЗЕФжЛгаЃЈ ЃЉ
A. ЂйЂкЂм B. ЂкЂл C. ЂлЂм D. ЂйЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЫЎЙћЯњЪлЭњМОЃЌФГЫЎЙћЕъЙКНјвЛгХжЪЫЎЙћЃЌНјМлЮЊ 20 дЊ/ЧЇПЫЃЌЪлМлВЛЕЭгк 20 дЊ/ЧЇПЫЃЌЧвВЛГЌЙ§ 32 дЊ/ЧЇПЫЃЌИљОнЯњЪлЧщПіЃЌЗЂЯжИУЫЎЙћвЛЬьЕФЯњЪлСП yЃЈЧЇПЫЃЉгыИУЬьЕФЪлМл xЃЈдЊ/ЧЇПЫЃЉТњзуШчЯТБэЫљЪОЕФвЛДЮКЏЪ§ЙиЯЕЃЎ
ЯњЪлСП yЃЈЧЇПЫЃЉ | Ё | 34.8 | 32 | 29.6 | 28 | Ё |
ЪлМл xЃЈдЊ/ЧЇПЫЃЉ | Ё | 22.6 | 24 | 25.2 | 26 | Ё |
(1)ФГЬьетжжЫЎЙћЕФЪлМлЮЊ 23.5 дЊ/ЧЇПЫЃЌЧѓЕБЬьИУЫЎЙћЕФЯњЪлСПЃЎ
(2)ШчЙћФГЬьЯњЪлетжжЫЎЙћЛёРћ 150 дЊЃЌФЧУДИУЬьЫЎЙћЕФЪлМлЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуDдкЁїABCЕФБпABЩЯЃЌЧвЁЯACDЃНЁЯAЃЎ
ЃЈ1ЃЉзїЁЯBDCЕФЦНЗжЯпDEЃЌНЛBCгкЕуEЃЎЃЈвЊЧѓЃКГпЙцзїЭМЃЌБЃСєзїЭМКлМЃЃЌЕЋВЛБиаДГізїЗЈЃЉЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЧѓжЄЃКDEЁЮACЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
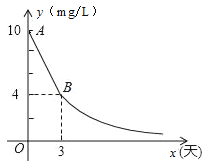
ЁОЬтФПЁПЛЗБЃОжЖдФГЦѓвЕХХЮлЧщПіНјааМьВтЃЌНсЙћЯдЪОЃКЫљХХЮлЫЎжаСђЛЏЮяЕФХЈЖШГЌБъЃЌМДСђЛЏЮяЕФХЈЖШГЌЙ§зюИпдЪаэЕФ1.0 mg/LЃЎЛЗБЃОжвЊЧѓИУЦѓвЕСЂМДећИФЃЌдк15ЬьвдФкЃЈКЌ15ЬьЃЉХХЮлДяБъЃЎећИФЙ§ГЬжаЃЌЫљХХЮлЫЎжаСђЛЏЮяЕФХЈЖШyЃЈmg/LЃЉгыЪБМфxЃЈЬьЃЉЕФБфЛЏЙцТЩШчЭМЫљЪОЃЌЦфжаЯпЖЮABБэЪОЧА3ЬьЕФБфЛЏЙцТЩЃЌЦфжаЕк3ЬьЪБСђЛЏЮяЕФХЈЖШНЕЮЊ4 mg/LЃЎДгЕк3ЬьЦ№ЫљХХЮлЫЎжаСђЛЏЮяЕФХЈЖШyгыЪБМфxТњзуЯТУцБэИёжаЕФЙиЯЕЃК
ЪБМфxЃЈЬьЃЉ | 3 | 4 | 5 | 6 | 8 | ЁЁ |
СђЛЏЮяЕФХЈyЃЈmg/LЃЉ | 4 | 3 | 2.4 | 2 | 1.5 |
ЃЈ1ЃЉЧѓећИФЙ§ГЬжаЕБ0Ёмx<3ЪБЃЌСђЛЏЮяЕФХЈЖШyгыЪБМфxЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЧѓећИФЙ§ГЬжаЕБxЁн3ЪБЃЌСђЛЏЮяЕФХЈЖШyгыЪБМфxЕФКЏЪ§БэДяЪНЃЛ
ЃЈ3ЃЉИУЦѓвЕЫљХХЮлЫЎжаСђЛЏЮяЕФХЈЖШЃЌФмЗёдк15ЬьвдФкВЛГЌЙ§зюИпдЪаэЕФ1.0 mg/LЃПЮЊЪВУДЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГіЯТСаЫЕЗЈЃЌЦфжае§ШЗЕФЪЧЃЈ ЃЉ
ЂйЙигк![]() ЕФвЛдЊЖўДЮЗНГЬ
ЕФвЛдЊЖўДЮЗНГЬ![]() ЃЌШє
ЃЌШє![]() ЃЌдђЗНГЬ
ЃЌдђЗНГЬ![]() вЛЖЈУЛгаЪЕЪ§ИљЃЛ
вЛЖЈУЛгаЪЕЪ§ИљЃЛ
ЂкЙигк![]() ЕФвЛдЊЖўДЮЗНГЬ
ЕФвЛдЊЖўДЮЗНГЬ![]() ЃЌШє
ЃЌШє![]() ЃЌдђЗНГЬ
ЃЌдђЗНГЬ![]() БигаЪЕЪ§ИљЃЛ
БигаЪЕЪ§ИљЃЛ
ЂлШє![]() ЪЧЗНГЬ
ЪЧЗНГЬ![]() ЕФИљЃЌдђ
ЕФИљЃЌдђ![]() ЃЛ
ЃЛ
ЂмШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊШ§НЧаЮШ§БпЃЌЗНГЬ
ЮЊШ§НЧаЮШ§БпЃЌЗНГЬ![]() гаСНИіЯрЕШЪЕЪ§ИљЃЌдђИУШ§НЧаЮЮЊжБНЧШ§НЧаЮЃЎ
гаСНИіЯрЕШЪЕЪ§ИљЃЌдђИУШ§НЧаЮЮЊжБНЧШ§НЧаЮЃЎ
A. ЂйЂк B. ЂйЂм C. ЂйЂкЂм D. ЂйЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕиЕие№ЧЃЖЏзХШЋЙњШЫУёЕФаФЃЌФГЕЅЮЛПЊеЙСЫЁАвЛЗНгаФбЃЌАЫЗНжЇдЎЁБътджОшПюЛюЖЏЃЎЕквЛЬьЪеЕНОшПю![]() дЊЃЌЕкШ§ЬьЪеЕНОшПю
дЊЃЌЕкШ§ЬьЪеЕНОшПю![]() дЊЃЎ
дЊЃЎ
![]() ШчЙћЕкЖўЬьЁЂЕкШ§ЬьЪеЕНОшПюЕФдіГЄТЪЯрЭЌЃЌЧѓОшПюдіГЄТЪЃП
ШчЙћЕкЖўЬьЁЂЕкШ§ЬьЪеЕНОшПюЕФдіГЄТЪЯрЭЌЃЌЧѓОшПюдіГЄТЪЃП
![]() АДее
АДее![]() жаЪеЕНОшПюЕФдіГЄТЪВЛБфЃЌИУЕЅЮЛШ§ЬьвЛЙВФмЪеЕНЖрЩйОшПюЃП
жаЪеЕНОшПюЕФдіГЄТЪВЛБфЃЌИУЕЅЮЛШ§ЬьвЛЙВФмЪеЕНЖрЩйОшПюЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊе§ЗНаЮDEFGЕФЖЅЕуDЁЂEдкЁїABCЕФБпBCЩЯЃЌЖЅЕуGЁЂFЗжБ№дкБпABЁЂACЩЯЃЎШчЙћBC=4ЃЌЁїABCЕФУцЛ§ЪЧ6ЃЌФЧУДетИіе§ЗНаЮЕФБпГЄЪЧ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌl1КЭl2ЗжБ№ЪЧзпЫНДЌКЭЮвЙЋАВПьЭЇКНааТЗГЬгыЪБМфЕФКЏЪ§ЭМЯѓЃЌЧыНсКЯЭМЯѓНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉдкИеГіЗЂЪБЃЌЮвЙЋАВПьЭЇОрзпЫНДЌЖрЩйКЃРяЃП
ЃЈ2ЃЉМЦЫузпЫНДЌгыЙЋАВЭЇЕФЫйЖШЗжБ№ЪЧЖрЩйЃП
ЃЈ3ЃЉЧѓГіl1ЃЌl2ЕФНтЮіЪНЃЎ
ЃЈ4ЃЉЮЪ6ЗжжгЪБЃЌзпЫНДЌгыЮвЙЋАВПьЭЇЯрОрЖрЩйКЃРяЃП

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com