
【题目】如图,l1和l2分别是走私船和我公安快艇航行路程与时间的函数图象,请结合图象解决下列问题:
(1)在刚出发时,我公安快艇距走私船多少海里?
(2)计算走私船与公安艇的速度分别是多少?
(3)求出l1,l2的解析式.
(4)问6分钟时,走私船与我公安快艇相距多少海里?

【答案】(1)5海里;(2)走私船:1海里/分;公安快艇:1.5海里/分(3)y1=t+5 ;y2=![]() ;(4)2海里;
;(4)2海里;
【解析】
(1)由图即可得出,我公安快艇距走私船的距离;
(2)根据路程除以时间即可求出速度;
(3)利用待定系数法即可求出一次函数的解析式;
(4)将t=6代入两个解析式求出各自路程,路程之差即为两艇之间的距离;
(1)在刚出发时我公安快艇距走私船5海里.
(2)公安快艇是4分钟6海里,走私船的速度(9-5) ÷4 =1海里/分;
公安快艇的速度是6÷4 = 1.5海里/分.
(3)设L1:y1 =k1t+b
∵过(0,5)和(4,9)点
∴5=b,9=4k1+b.
解得 k1=1,b=5 .
∴y1=t+5 .
设L2:y2=k2t∵过(4,6)点,∴6=4k.
∴k=![]()
∴y2=![]()
(4)当t=6时,y1=11,y2=9;11-9=2
∴6分钟时相距2海里.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过D作DE⊥AC于E,AB-BC=4,AC=8,则△ABP面积为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ACB中,∠BAC=90°,AB=AC,分别过B、C两点作过点A的直线l的垂线,垂足为D、E;
(1)如图1,当D、E两点在直线BC的同侧时,猜想,BD、CE、DE三条线段有怎样的数量关系?并说明理由.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

(3)如图3,∠BAC=90°,AB=25,AC=35.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等?(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的纸片,长AD=10厘米,宽AB=8厘米,AD沿点A对折,点D正好落在BC上的点F处,AE是折痕。
(1)图中有全等的三角形吗?如果有,请直接写出来;
(2)求线段BF的长;
(3)求线段EF的长;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某学校初四年纪学生每周平均课外阅读时间的情况,随机抽查了该学校初四年级m名同学,对其每周平均课外阅读时间进行统计,绘制了如下条形统计图(图一)和扇形统计图(图二):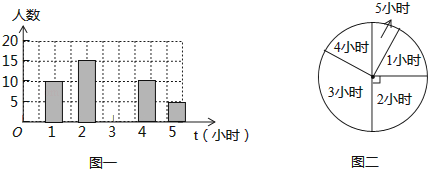
(1)根据以上信息回答下列问题:
①求m值.
②求扇形统计图中阅读时间为5小时的扇形圆心角的度数.
③补全条形统计图.
(2)直接写出这组数据的众数、中位数,求出这组数据的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用(-1,0)表示A点的位置,用(2,1)表示B点的位置,那么:

(1)画出直角坐标系。
(2)写出△DEF的三个顶点的坐标。
(3)在图中表示出点M(6,2),N(4,4)的位置。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为 . 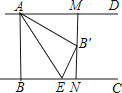
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求回答问题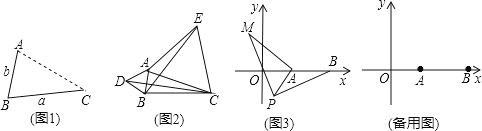
(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.
当点A位于时,线段AC的长取得最大值,且最大值为(用含a,b的式子表示)
(2)应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.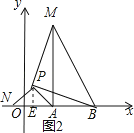
(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下面是利用尺规作∠AOB的角平分线OC的作法:
①以点O为圆心,任意长为半径作弧,交OA、OB于点D,E;
②分别以点D,E为圆心,以大于![]() DE的长为半径作弧,两弧在∠AOB内部交于点C;
DE的长为半径作弧,两弧在∠AOB内部交于点C;
③作射线OC,则射线OC就是∠AOB的平分线.
以上用尺规作角平分线时,用到的三角形全等的判定方法是( )

A. SSS B. SAS
C. ASA D. AAS
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com