
ЁОЬтФПЁПШчЭМ1ЃЌдкRtЁїACBжаЃЌЁЯBAC=90ЁуЃЌAB=ACЃЌЗжБ№Й§BЁЂCСНЕузїЙ§ЕуAЕФжБЯпlЕФДЙЯпЃЌДЙзуЮЊDЁЂEЃЛ
ЃЈ1ЃЉШчЭМ1ЃЌЕБDЁЂEСНЕудкжБЯпBCЕФЭЌВрЪБЃЌВТЯыЃЌBDЁЂCEЁЂDEШ§ЬѕЯпЖЮгадѕбљЕФЪ§СПЙиЯЕЃПВЂЫЕУїРэгЩЃЎ
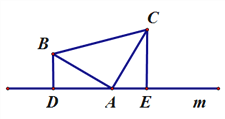
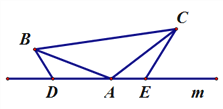
ЃЈ2ЃЉШчЭМЃЈ2ЃЉЃЌНЋЃЈ1ЃЉжаЕФЬѕМўИФЮЊЃКдкЁїABCжаЃЌAB=ACЃЌDЁЂAЁЂEШ§ЕуЖМдкжБЯпmЩЯЃЌВЂЧвгаЁЯBDA=ЁЯAEC=ЁЯBAC=ІСЃЌЦфжаІСЮЊШЮвтШёНЧЛђЖлНЧЃЎЧыЮЪНсТлDE=BD+CEЪЧЗёГЩСЂЃПШчГЩСЂЃЌЧыФуИјГіжЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ

ЃЈ3ЃЉШчЭМ3ЃЌЁЯBAC=90ЁуЃЌAB=25ЃЌAC=35ЃЎЕуPДгBЕуГіЗЂбиBЁњAЁњCТЗОЖЯђжеЕуCдЫЖЏЃЛЕуQДгCЕуГіЗЂбиCЁњAЁњBТЗОЖЯђжеЕуBдЫЖЏЃЎЕуPКЭQЗжБ№вдУПУы2КЭ3ИіЕЅЮЛЕФЫйЖШЭЌЪБПЊЪМдЫЖЏЃЌжЛвЊгавЛЕуЕНДяЯргІЕФжеЕуЪБСНЕуЭЌЪБЭЃжЙдЫЖЏЃЛдкдЫЖЏЙ§ГЬжаЃЌЗжБ№Й§PКЭQзїPFЁЭlгкFЃЌQGЁЭlгкGЃЎЮЪЃКЕуPдЫЖЏЖрЩйУыЪБЃЌЁїPFAгыЁїQAGШЋЕШЃПЃЈжБНгаДГіД№АИЃЉ
ЁОД№АИЁП(1)BD+ CE = DEЃЛ (2)ГЩСЂЃЛЃЈ3ЃЉЕуPдЫЖЏ10Лђ12Уы.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉ)BD+ CE = DEЃЌИљОнЁЯBDA=ЁЯCEA=90ЁуЃЌжЄЕУЁЯEAC=ЁЯABDЃЌРћгУAASжЄУїЁїABDЁеЁїACEЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪПЩЕУAD=CEЃЌBD=AEЃЌЫљвдDE=BD+CEЃЛ
ЃЈ2ЃЉГЩСЂЃЌРћгУЁЯBDA=ЁЯBAC=ІСЃЌдђЁЯDBA+ЁЯBAD=ЁЯBAD+ЁЯCAE=180Ёу-ІСЃЌЕУГіЁЯCAE=ЁЯABDЃЌНјЖјжЄЕУЁїADBЁеЁїCEAЃЌМДПЩЕУГіД№АИЃЎ
ЃЈ3ЃЉИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНМДПЩЧѓЕУЃЛ
ЃЈ4ЃЉвзжЄЁЯPFA=ЁЯQGAЃЌЁЯPAF=ЁЯAQGЃЌжЛашPA=QAЃЌОЭПЩЕУЕНЁїPFAгыЁїQAGШЋЕШЃЌШЛКѓжЛашИљОнЕуPКЭЕуQВЛЭЌЮЛжУНјааЗжРрЬжТлМДПЩНтОіЮЪЬтЃЎ
ЪдЬтНтЮіЃК
(1)BD+DE=CE
жЄЃКЁпBDЁЭжБЯпlЃЌCEЁЭжБЯпlЃЌ
ЁпBDЁЭlЃЌCEЁЭl
ЁрЁЯBDA=ЁЯCEA=90Ёу
ЁрЁЯABD+ЁЯDAB=90Ёу
ЁпЁЯBAC=90Ёу
ЁрЁЯDAB+ЁЯCAE=90Ёу
ЁрЁЯABD=ЁЯCAE
дкЁїABDКЭЁїCAEжаЃЌ
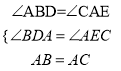
ЁрЁїABDЁеЁїCAEЃЈAASЃЉЃЌ
ЁрAD=CEЃЌBD=AEЃЎ
ЁпDE=AD+AEЃЌ
ЁрDE=CE+BDЃЛ
(2)ГЩСЂ
жЄЃКЁпЁЯCAE=180Ёу-ЁЯBAC-ЁЯBAD
ЁЯDBA=180Ёу-ЁЯBDA-ЁЯBAD
ЁпЁЯBAC=ЁЯBDA
ЁрЁЯCAE=ЁЯABD
дкЁїABDКЭЁїCAEжаЃЌ
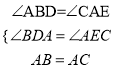
ЁрЁїABDЁеЁїCAEЃЈAASЃЉЃЌ
ЁрAD=CEЃЌBD=AEЃЎ
ЁпDE=AD+AEЃЌ
ЁрDE=CE+BDЃЛ

ЃЈ3ЃЉЕуPдЫЖЏ10Лђ12Уы.


 еуНжЎаЧПЮЪБгХЛЏзївЕЯЕСаД№АИ
еуНжЎаЧПЮЪБгХЛЏзївЕЯЕСаД№АИ МЄЛюЫМЮЌгХМгПЮЬУЯЕСаД№АИ
МЄЛюЫМЮЌгХМгПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћ|y+3|+ЃЈ2xЉ4ЃЉ2=0ЃЌФЧУД2xЉyЕФжЕЮЊЃЈ ЃЉ
A.1
B.Љ1
C.Љ7
D.7
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСтаЮВЛОпБИЕФаджЪЪЧЃЈЁЁЁЁЃЉ
A.ЖдНЧЯпвЛЖЈЯрЕШB.ЖдНЧЯпЛЅЯрДЙжБ
C.ЪЧжсЖдГЦЭМаЮD.ЪЧжааФЖдГЦЭМаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбДЦкЕФФГвЛЬь,ФГЫЎПтЩЯЮч8ЪБЕФЫЎЮЛЪЧ45mЫцКѓЫЎЮЛвдУПаЁЪБ0.6mЕФЫйЖШЩЯеЧ,жаЮч12ЪБПЊЪМПЊеЂаЙКщ,жЎКѓЫЎЮЛвдУПаЁЪБ0.3mЕФЫйЖШЯТНЕ,дђЕБЬьЯТЮч6ЪБ,ИУЫЎПтЕФЫЎЮЛЪЧЃЈ ЃЉ
A. 45.4m B. 45.6m C. 45.8m D. 46m
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаИїЬте§ШЗЕФЪЧЃЈ ЃЉ
A.3x+3y=6xy
B.x+x=x2
C.Љ9y2+6y2=Љ3
D.9a2bЉ9a2b=0
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаРэЪ§aЃЌbдкЪ§жсЩЯЕФЮЛжУШчЭМЫљЪОЃЌдђЯТСаНсТлжаЃЌВЛе§ШЗЕФЪЧЃЈ ЃЉ ![]()
A.a+bЃМ0
B.aЉbЃО0
C.![]() ЃМ0
ЃМ0
D.|a|ЃО|b|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
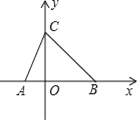
ЁОЬтФПЁПШчЭМЃЌЕуAЮЊxжсИКАыжсЩЯвЛЕуЃЌЕуBЮЊxжсе§АыжсЩЯвЛЕуЃЌOAЁЂOBЃЈOAЃМ0BЃЉЕФГЄЗжБ№ЪЧЙигкxЕФвЛдЊЖўДЮЗНГЬx2Љ4mx+m2+2=0ЕФСНИљЃЌCЃЈ0ЃЌ3ЃЉЃЌЧвЁїABCЕФУцЛ§ЮЊ6ЃЌЧѓЁЯABCЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіШ§НЧаЮШ§БпжЎБШЮЊ3ЃК5ЃК7ЃЌгыЫќЯрЫЦЕФШ§НЧаЮЕФзюГЄБпЮЊ21cmЃЌдђЦфгрСНБпжЎКЭЮЊЃЈЁЁЁЁЃЉ
A.24cm
B.21cm
C.13cm
D.9cm
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌCDЪЧБпABЩЯЕФИпЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїACDЁзЁїCBDЃЛ
ЃЈ2ЃЉЧѓЁЯACBЕФДѓаЁЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com