
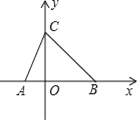
【题目】如图,点A为x轴负半轴上一点,点B为x轴正半轴上一点,OA、OB(OA<0B)的长分别是关于x的一元二次方程x2﹣4mx+m2+2=0的两根,C(0,3),且△ABC的面积为6,求∠ABC的度数.
【答案】∠ABC=45°.
【解析】试题分析:先根据三角形ABC的面积求出AB的值,再由根与系数的关系就可以求出m的值,从而求出方程的解,就可以得出OB的值,进而得出△OBC为等腰直角三角形就可以得出结论.
试题解析:∵C(0,3),
∴CO=3.
∵△ABC的面积为6,
∴![]() =6,∴AB=4,
=6,∴AB=4,
∵OA、OB(OA<0B)的长分别是关于x的一元二次方程x2﹣4mx+m2+2=0的两根,
∴OA+OB=4m,∴4m=4,∴m=1,
∴一元二次方程为:x2﹣4x+3=0,∴x1=1,x2=3,
∵OA<0B,∴OA=1,OB=3.∴OB=OC,
∴△OBC是等腰直角三角形,
∴∠ABC=45°,
答:∠ABC=45°.


科目:初中数学 来源: 题型:
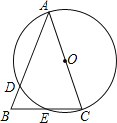
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ACB中,∠BAC=90°,AB=AC,分别过B、C两点作过点A的直线l的垂线,垂足为D、E;
(1)如图1,当D、E两点在直线BC的同侧时,猜想,BD、CE、DE三条线段有怎样的数量关系?并说明理由.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

(3)如图3,∠BAC=90°,AB=25,AC=35.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等?(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里.
﹣4,﹣|﹣ ![]() |,0,
|,0, ![]() ,﹣3.14,2006,﹣(+5),+1.88
,﹣3.14,2006,﹣(+5),+1.88
(1)正数集合:{};
(2)负数集合:{};
(3)整数集合:{};
(4)分数集合:{}.
查看答案和解析>>
科目:初中数学 来源: 题型:
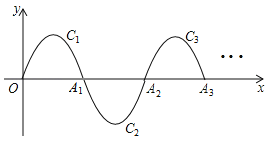
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com