
【题目】已知四边形ABCD是正方形,等腰直角△AEF的直角顶点E在BC上,(不与B、C重合),FM⊥AD,交射线AD于点M.
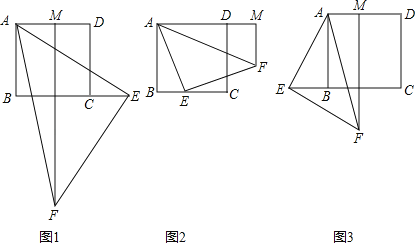
(1)如图1,当点E在边BC的延长线上,点M在边AD上时,请直接写出线段AB,BE,AM之间的数量关系,不需要证明.
(2)如图2,当点E在边BC上,点M在边AD的延长线上时,请写出线段AB,BE,AM之间的数量关系,并且证明你的结论.
(3)如图3,当点E在边CB的延长线上,点M在边AD上时,若BE=![]() ,∠AFM=15°,求AM的长度.
,∠AFM=15°,求AM的长度.
【答案】(1)AB+AM=BE;(2)AM=BE+AB;(3)AM=3﹣![]() .
.
【解析】
(1)证明△ABE≌△EHF(AAS),可得结论:BE=AM+AB;
(2)根据AAS证明△ABE≌△EHF,可得结论:AM=BE+AB;
(3)首先由∠AFM=15°,易得∠EAB=30°,由△ABE≌△EHF,根据全等三角形的性质易得AB=EH,利用锐角三角函数易得AB,最后可以计算AM的长.
(1)AB+AM=BE.理由是:如图1,
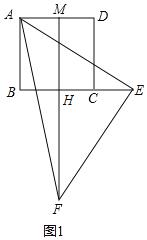
∵四边形ABCD是正方形
∴∠ABC=∠BAD=90°
∴∠BAE+∠AEB=90°,
∵∠AEF=∠AEB+∠HEF=90°,
∴∠BAE=∠HEF,
在△ABE与△EHF中,
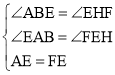 ,
,
∴△ABE≌△EHF(AAS),
∴AB=EH,
∵FM⊥AD,
∴∠AMH=∠BAD=∠ABC=90°,
∴四边形ABHM是矩形,
∴AM=BH,
∴BE=BH+EH=AM+AB;
(2)如图2,AM=BE+AB.
证明:延长MF,交BC延长线于H,
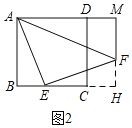
∵四边形ABCD为正方形,
∴∠BAM=∠B=90°,
∵FM⊥AD,
∴∠AMF=90°,
∴四边形ABHM为矩形,
∴AM=BH,
∵△AEF是等腰直角三角形,
∴AE=EF,∠AEF=90°,
∴∠AEB+∠FEH=90°,
∵∠B=90°,
∴∠AEB+∠BAE=90°,
∴∠FEH=∠BAE,
∵∠B=∠EHF=90°,
∴△ABE≌△EHF(AAS),
∴AB=EH,
∴AM=BH=BE+EH=BE+AB.
(3)如图3,FM与BC相交于H.
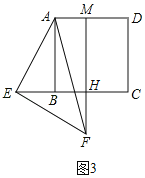
∵△AEF是等腰直角三角形,
∴AE=EF,∠AEF=90°,
∴∠EAF=45°,
同理得:四边形ABHM是矩形,
∴AM=BH,
∵AB∥FM,
∴∠BAF=∠AFM=15°,
∴∠BAE=∠EAF﹣∠BAF=45°﹣15°=30°.
在Rt△ABE中,BE=![]() ,
,
AB=![]() BE=3.
BE=3.
同理得:△ABE≌△EHF,
∴EH=AB=3,
∴BH=EH﹣BE=3﹣![]() ,
,
∴AM=BH=3﹣![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
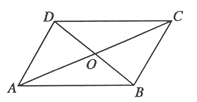
【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD//BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学设计的“已知底边及底边上的高作等腰三角形”的尺规作图的过程.
已知:如图1,线段a和线段b.
求作:△ABC,使得AB=AC,BC=a,BC边上的高为b.
作法:如图2,
①作射线BM,并在射线BM上截取BC=a;
②作线段BC的垂直平分线PQ,PQ交BC于D;
③以D为圆心,b为半径作圆,交PQ于A;
④连接AB和AC.
则△ABC就是所求作的图形.
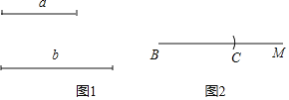
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图2中的图形;
(2)完成下面的证明:
证明:由作图可知BC=a,AD=b.
∵PQ为线段BC的垂直平分线,点A在PQ上,
∴AB=AC(______)(填依据).
又∵AD在线段BC的垂直平分线PQ上,
∴AD⊥BC.
∴AD为BC边上的高,且AD=b.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,A,B分别在射线OM,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点.
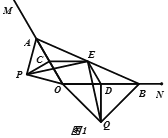
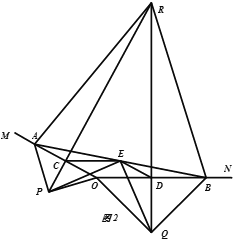
(1)求证:四边形OCED为平行四边形;
(2)求证:△PCE≌△EDQ
(3)如图2,延长PC,QD交于点R.若∠MON=150°,求证:△ABR为等边三角形。
查看答案和解析>>
科目:初中数学 来源: 题型:
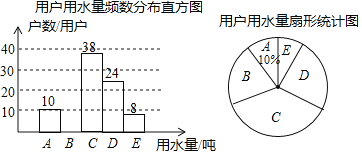
【题目】我市为了节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费为更好地决策,自来水公司在某街道随机抽取了部分用户的用水量数据,按A,B,C,D,E五个区间进行统计,并将统计结果绘制如下两幅不完整的统计图,请你结合图中所给信息解答下列问题:(说明:A:0﹣3吨;B:3﹣6吨;C:6﹣9吨;D:9﹣12吨;E:12﹣16吨,且每组数据区间包括右端的数但不包括左端的数)
(1)这次随机抽样调查了_____用户
(2)补全频数分布直方图,求扇形统计图中B部分的圆心角的度数;
(3)如果自来水公司将基本用水量定为每户9吨,那么该街道1.8万用户中约有多少用户的用水全部享受基本用水量的价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
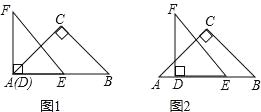
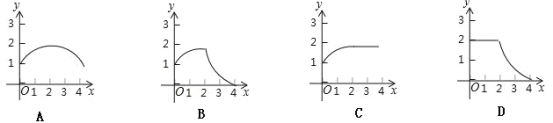
【题目】如图1,△ABC和△DEF都是等腰直角三角形,其中∠C=∠EDF=90°,点A与点D重合,点E在AB上,AB=4,DE=2.如图2,△ABC保持不动,△DEF沿着线段AB从点A向点B移动,当点D与点B重合时停止移动.设AD=x,△DEF与△ABC重叠部分的面积为y,则y关于x的函数图象大致是( )
查看答案和解析>>
科目:初中数学 来源: 题型:
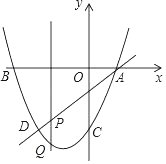
【题目】如图,抛物线y=x2+bx﹣3过点A(1,0),直线AD交抛物线于点D,点D的横坐标为﹣2,点P是线段AD上的动点.
(1)b= ,抛物线的顶点坐标为 ;
(2)求直线AD的解析式;
(3)过点P的直线垂直于x轴,交抛物线于点Q,连接AQ,DQ,当△ADQ的面积等于△ABD的面积的一半时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
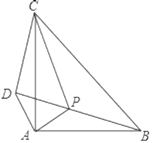
【题目】如图所示,在等腰Rt△ABC中,∠CAB=90°,P是△ABC内一点,将△PAB绕A逆时针旋转90°得△DAC.
(1)试判断△PAD的形状并说明理由;
(2)连接PC,若∠APB=135°,PA=1,PB=3,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AD于点E,交BC于点F,连接BE,DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com