
【题目】已知△ABC是等腰直角三角形,AB=AC,D为平面内的任意一点,且满足CD=AC,若△ADB是以AD为腰的等腰三角形,则∠CDB的度数为_____.
【答案】45°或135°.
【解析】
当△ADB是以AD为腰的等腰三角形,可以分两种情况进行讨论:①AD=AB,②AD=BD;
①当AD=AB时,又分两种情况:
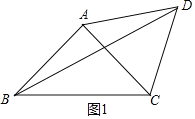
当点D在AC边上方时,如图1所示.由△ACD为等边三角形,得∠CAD=60°,根据角的关系可得结论;
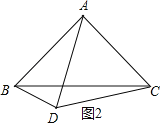
当点D在AC边下方时,如图2所示.同理可得结论;
②当AD=BD时又分两种情况:
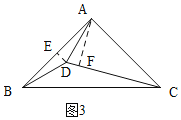
当点D在BC的上方,如图3所示.作辅助线,证明∠EDA=∠ADC,根据角平分线的性质得:AF=AE=![]() AB=
AB=![]() AC,利用直角三角形30°角的判定得:Rt△AFC中,∠ACF=30°,从而得出结论;
AC,利用直角三角形30°角的判定得:Rt△AFC中,∠ACF=30°,从而得出结论;
当D在BC的下方时,如图4,同理构建矩形AEFC,由CF=![]() AB=
AB=![]() AC=
AC=![]() CD,得Rt△CFD中,∠CDF=30°,可得结论.
CD,得Rt△CFD中,∠CDF=30°,可得结论.
解:①当AD=AB时,
∵AB=AC,CD=AC,AD=AB,
∴AC=AD=CD,
∴△ACD为等边三角形.
当点D在AC边上方时,如图1所示.
∵△ABC是等腰直角三角形,AB=AC,△ACD为等边三角形,
∴∠BAC=90°,∠CAD=60°,
∴∠BAD=∠BAC+∠CAD=150°.
∵AB=AD,
∴∠ABD=∠ADB=![]() (180°﹣∠BAD)=15°,
(180°﹣∠BAD)=15°,
∴∠CDB=∠ADC﹣∠ADB=60°﹣15°=45°;
当点D在AC边下方时,如图2所示.
∵∠BAC=90°,∠CAD=60°,
∴∠BAD=∠BAC﹣∠CAD=30°.
∵AB=AD,
∴∠ABD=∠ADB=![]() (180°﹣∠BAD)=75°,
(180°﹣∠BAD)=75°,
∴∠CDB=∠ADB+∠ADC=75°+60°=135°.
②当AD=BD时,
当点D在BC的上方,如图3所示.
过D作DE⊥AB于E,过A作AF⊥CD于F,
∴∠BED=90°,
∵∠BAC=90°,
∴∠BED=∠BAC,
∴ED∥AC,
∴∠EDA=∠DAC,
∵AD=CD,
∴∠ADC=∠DAC,
∴∠EDA=∠ADC,
∴AF=AE=![]() AB=
AB=![]() AC,
AC,
Rt△AFC中,∠ACF=30°,
∴∠ADC=![]() =75°,
=75°,
∴∠ADB=2∠ADE=2∠ADC=150°,
∴∠CDB=360°﹣150°﹣75°=135°;
当D在BC的下方时,如图4,
过D作DE⊥AC于E,过C作CF⊥ED于F,
∴∠AEF=∠BAC=∠EFC=90°,
∴四边形AEFC是矩形,
∴CF=AE,
∵AD=BD,DE⊥AB,
∴AE=![]() AB,∠ADE=∠BDE,
AB,∠ADE=∠BDE,
∴CF=![]() AB=
AB=![]() AC=
AC=![]() CD,
CD,
Rt△CFD中,∠CDF=30°,
∵AC∥ED,
∴∠CAD=∠ADE,
∵AC=CD,
∴∠CAD=∠ADC,
∴∠CDA=∠ADE=![]() ∠CDF=15°,
∠CDF=15°,
∴∠ADB=30°,
∴∠CDB=45°.
综上所述,则∠CDB的度数为45°或135°;
故答案为:45°或135°.



 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,AD=4![]() ,点E是BC的中点,点F在AB上,FB=2,P是矩形上一动点.若点P从点F出发,沿F→A→D→C的路线运动,当∠FPE=30°时,FP的长为_____.
,点E是BC的中点,点F在AB上,FB=2,P是矩形上一动点.若点P从点F出发,沿F→A→D→C的路线运动,当∠FPE=30°时,FP的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对博鳌论坛会的了解情况,某中学随机抽取了部分学生进行问卷调查,将调查结果记作“![]() 非常了解,
非常了解,![]() 了解,
了解,![]() 了解较少,
了解较少,![]() 不了解.”四类分别统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
不了解.”四类分别统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
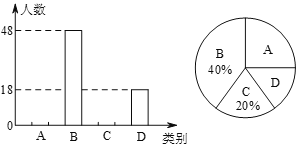
(1)此次共调查了______名学生;扇形统计图中![]() 所在的扇形的圆心角度数为______;
所在的扇形的圆心角度数为______;
(2)将条形统计图补充完整;
(3)若该校共有1600名学生,请你估计对博鳌论坛会的了解情况为“非常了解”的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新能源汽车的发展,某公交公司将用新能源公交车淘汰某一条线路上“冒黑烟”较严重的燃油公交车,计划购买A型和B型新能源公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需300万元;若购买A型公交车2辆,B型公交车1辆,共需270万元,
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为80万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1000万元,且确保这10辆公交车在该线路的年均载客量总和不少于900万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类别,每位同学仅选一项.根据调査结果绘制了不完整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | a | 0.5 |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | b | 1 |
根据图表提供的信息,回答下列问题:
(1)直接写出:a= .b= m= ;
(2)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请求选取的2人恰好是甲和乙的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作发现)
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.

(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;
(2)在(1)所画图形中,∠AB′B=____.
(问题解决)
(3)如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
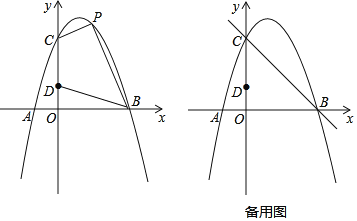
【题目】如图,对称轴为直线x=1的抛物线经过A(﹣1,0)、C(0,3)两点,与x轴的另一个交点为B,点D在y轴上,且OB=3OD
(1)求该抛物线的表达式;
(2)设该抛物线上的一个动点P的横坐标为t
①当0<t<3时,求四边形CDBP的面积S与t的函数关系式,并求出S的最大值;
②点Q在直线BC上,若以CD为边,点C、D、Q、P为顶点的四边形是平行四边形,请求出所有符合条件的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com