
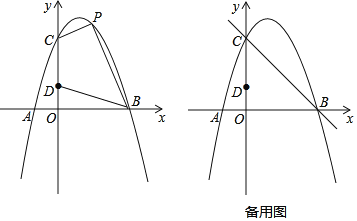
【题目】如图,对称轴为直线x=1的抛物线经过A(﹣1,0)、C(0,3)两点,与x轴的另一个交点为B,点D在y轴上,且OB=3OD
(1)求该抛物线的表达式;
(2)设该抛物线上的一个动点P的横坐标为t
①当0<t<3时,求四边形CDBP的面积S与t的函数关系式,并求出S的最大值;
②点Q在直线BC上,若以CD为边,点C、D、Q、P为顶点的四边形是平行四边形,请求出所有符合条件的点P的坐标.
【答案】(1)y=﹣x2+2x+3(2)①t=![]() 时,S的最大值为
时,S的最大值为![]() ②P(1,4)或(2,3)或(
②P(1,4)或(2,3)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)设所求抛物线的表达式为 y=a(x+1)(x﹣3),把点C(0,3)代入表达式,即可求解;
(2)①设P(t,﹣t2+2t+3),则E(t,﹣t+3),S四边形CDBP=S△BCD+S△BPC=![]() CDOB+
CDOB+![]() PEOB,即可求解;
PEOB,即可求解;
②分点P在点Q上方、下方两种情况讨论即可求解.
(1)∵抛物线的对称轴为x=1,A(﹣1,0),
∴B(3,0).
∴设所求抛物线的表达式为 y=a(x+1)(x﹣3),
把点C(0,3)代入,得3=a(0+1)(0﹣3),
解得a=﹣1,
∴所求抛物线的表达式为y=﹣(x+1)(x﹣3),即y=﹣x2+2x+3;
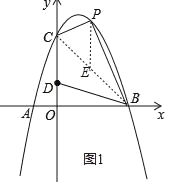
(2)①连结BC.
∵B(3,0),C(0,3),
∴直线BC的表达式为y=﹣x+3,
∵OB=3OD,OB=OC=3,
∴OD=1,CD=2,
过点P作PE∥y轴,交BC于点E(如图1).
设P(t,﹣t2+2t+3),则E(t,﹣t+3).
∴PE=﹣t2+2t+3﹣(﹣t+3)=﹣t2+3t.
S四边形CDBP=S△BCD+S△BPC=![]() CDOB+
CDOB+![]() PEOB,
PEOB,
即S=![]() ×2×3+
×2×3+![]() (﹣t2+3t)×3=﹣
(﹣t2+3t)×3=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∵a=﹣![]() <0,且0<t<3,
<0,且0<t<3,
∴当t=![]() 时,S的最大值为
时,S的最大值为![]() ;
;
②以CD为边,点C、D、Q、P为顶点的四边形是平行四边形,
则PQ∥CD,且PQ=CD=2.
∵点P在抛物线上,点Q在直线BC上,
∴点P(t,﹣t2+2t+3),点Q(t,﹣t+3).
分两种情况讨论:
(Ⅰ) 如图2,当点P在点Q上方时,
∴(﹣t2+2t+3)﹣(﹣t+3)=2.即t2﹣3t+2=0.解得 t1=1,t2=2.
∴P1(1,4),P2(2,3),
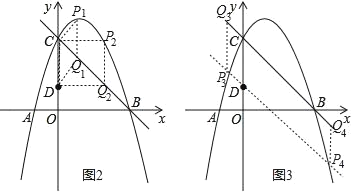
(Ⅱ) 如图3,当点P在点Q下方时,
∴(﹣t+3)﹣(﹣t2+2t+3)=2.即t2﹣3t﹣2=0.
解得 t3=![]() ,t4=
,t4=![]() ,
,
∴P3(![]() ,
,![]() ),P4(
),P4(![]() ,
,![]() ),
),
综上所述,所有符合条件的点P的坐标分别为:P(1,4)或(2,3)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】已知△ABC是等腰直角三角形,AB=AC,D为平面内的任意一点,且满足CD=AC,若△ADB是以AD为腰的等腰三角形,则∠CDB的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
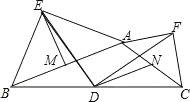
【题目】如图,在钝角三角形![]() 中,分别以
中,分别以![]() 和
和![]() 为斜边向
为斜边向![]() 的外侧作等腰直角三角形
的外侧作等腰直角三角形![]() 和等腰直角三角形
和等腰直角三角形![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,取
,取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确结论有( )
.其中正确结论有( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,以AB为直径的OO与BC相交于点D,与AC相交于点E,DF⊥AC,垂足为F,连接DE,过点A作AG⊥DE,垂足为G,AG与⊙O交于点H.
(1)求证:DF是⊙O的切线;
(2)若∠CAG=25°,求弧AH的长;
(3)若tan∠CDF=![]() ,求AE的长;
,求AE的长;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校1200名学生发起向贫困山区学生捐款活动,为了解捐款情况,学生会随机抽取了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②.
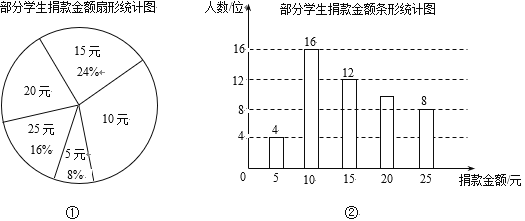
请根据以上信息,解答下列问题:
(1)本次抽样调查的样本容量为____;
(2)图①中“20元”对应扇形的圆心角的度数为_____°;
(3)估计该校本次活动捐款金额为15元以上(含15元)的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“大美湿地,水韵盐城”.某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:

请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有800名学生,请估计“最想去景点B“的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com