
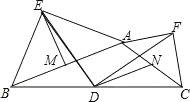
【题目】如图,在钝角三角形![]() 中,分别以
中,分别以![]() 和
和![]() 为斜边向
为斜边向![]() 的外侧作等腰直角三角形
的外侧作等腰直角三角形![]() 和等腰直角三角形
和等腰直角三角形![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,取
,取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确结论有( )
.其中正确结论有( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
【答案】D
【解析】
①首先根据D是BC中点,N是AC中点N,可得DN是△ABC的中位线,判断出DN=![]() AB;然后判断出EM=
AB;然后判断出EM=![]() AB,即可判断出EM=DN;
AB,即可判断出EM=DN;
②首先根据DN∥AB,可得△CDN∽ABC;然后根据DN=![]() AB,可得S△CDN=
AB,可得S△CDN=![]() S△ABC,所以S△CDN=
S△ABC,所以S△CDN=![]() S四边形ABDN,据此判断即可.
S四边形ABDN,据此判断即可.
③首先连接MD、FN,判断出DM=FN,∠EMD=∠DNF,然后根据全等三角形判定的方法,判断出△EMD≌△DNF,即可判断出DE=DF.
④首先判断出![]() =sin45°=
=sin45°=![]() ,DM=
,DM=![]() FA,∠EMD=∠EAF,根据相似三角形判定的方法,判断出△EMD∽△∠EAF,即可判断出∠MED=∠AEF,然后根据∠MED+∠AED=45°,判断出∠DEF=45°,再根据DE=DF,判断出∠DFE=45°,∠EDF=90°,即可判断出DE⊥DF.
FA,∠EMD=∠EAF,根据相似三角形判定的方法,判断出△EMD∽△∠EAF,即可判断出∠MED=∠AEF,然后根据∠MED+∠AED=45°,判断出∠DEF=45°,再根据DE=DF,判断出∠DFE=45°,∠EDF=90°,即可判断出DE⊥DF.
解:∵D是BC中点,N是AC中点,
∴DN是△ABC的中位线,
∴DN∥AB,且DN=![]() AB;
AB;
∵三角形ABE是等腰直角三角形,EM平分∠AEB交AB于点M,
∴M是AB的中点,
∴EM=![]() AB,
AB,
又∵DN=![]() AB,
AB,
∴EM=DN,
∴结论①正确;
∵DN∥AB,
∴△CDN∽ABC,
∵DN=![]() AB,
AB,
∴S△CDN=![]() S△ABC,
S△ABC,
∴S△CDN=![]() S四边形ABDN,
S四边形ABDN,
∴结论②正确;
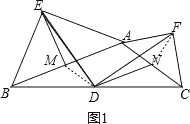
如图1,连接MD、FN,
∵D是BC中点,M是AB中点,
∴DM是△ABC的中位线,
∴DM∥AC,且DM=![]() AC;
AC;
∵三角形ACF是等腰直角三角形,N是AC的中点,
∴FN=![]() AC,
AC,
又∵DM=![]() AC,
AC,
∴DM=FN,
∵DM∥AC,DN∥AB,
∴四边形AMDN是平行四边形,
∴∠AMD=∠AND,
又∵∠EMA=∠FNA=90°,
∴∠EMD=∠DNF,
在△EMD和△DNF中,
EM=DN,∠EMD=∠DNF,MD=NF,
∴△EMD≌△DNF,
∴DE=DF,
∴结论③正确;
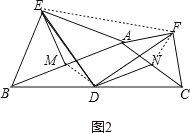
如图2,连接MD,EF,NF,
∵三角形ABE是等腰直角三角形,EM平分∠AEB,
∴M是AB的中点,EM⊥AB,
∴EM=MA,∠EMA=90°,∠AEM=∠EAM=45°,
∴![]() =sin45°=
=sin45°=![]() ,
,
∵D是BC中点,M是AB中点,
∴DM是△ABC的中位线,
∴DM∥AC,且DM=![]() AC;
AC;
∵三角形ACF是等腰直角三角形,N是AC的中点,
∴FN=![]() AC,∠FNA=90°,∠FAN=∠AFN=45°,
AC,∠FNA=90°,∠FAN=∠AFN=45°,
又∵DM=![]() AC,
AC,
∴DM=FN=![]() FA,
FA,
∵∠EMD=∠EMA+∠AMD=90°+∠AMD,
∠EAF=360°∠EAM∠FAN∠BAC
=360°45°45°(180°∠AMD)
=90°+∠AMD
∴∠EMD=∠EAF,
在△EMD和△∠EAF中,![]() ,∠EMD=∠EAF,
,∠EMD=∠EAF,
∴△EMD∽△∠EAF,
∴∠MED=∠AEF,
∵∠MED+∠AED=45°,
∴∠AED+∠AEF=45°,
即∠DEF=45°,
又∵DE=DF,
∴∠DFE=45°,
∴∠EDF=180°45°45°=90°,
∴DE⊥DF,
∴结论④正确.
∴正确的结论有4个:①②③④.
故选:D.


科目:初中数学 来源: 题型:
【题目】为了解学生对博鳌论坛会的了解情况,某中学随机抽取了部分学生进行问卷调查,将调查结果记作“![]() 非常了解,
非常了解,![]() 了解,
了解,![]() 了解较少,
了解较少,![]() 不了解.”四类分别统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
不了解.”四类分别统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
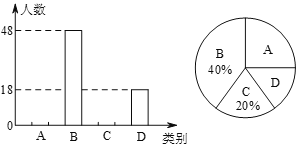
(1)此次共调查了______名学生;扇形统计图中![]() 所在的扇形的圆心角度数为______;
所在的扇形的圆心角度数为______;
(2)将条形统计图补充完整;
(3)若该校共有1600名学生,请你估计对博鳌论坛会的了解情况为“非常了解”的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作发现)
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.

(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;
(2)在(1)所画图形中,∠AB′B=____.
(问题解决)
(3)如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
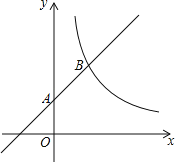
【题目】如图,在平面直角坐标系中,一次函数y=x+b的图象经过点A(0,1),与反比例函数y=![]() (x>0)的图象交于B(m,2).
(x>0)的图象交于B(m,2).
(1)求k和b的值;
(2)在双曲线y=![]() (x>0)上是否存在点C,使得△ABC为等腰直角三角形?若存在,求出点C坐标;若不存在,请说明理由.
(x>0)上是否存在点C,使得△ABC为等腰直角三角形?若存在,求出点C坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
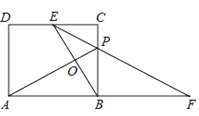
【题目】如图,矩形ABCD中,E为DC的中点,AD:AB=![]() :2,CP:BP=1:2,连接EP并延长,交AB的延长线于点F,AP、BE相交于点O.下列结论:①EP平分∠CEB;②
:2,CP:BP=1:2,连接EP并延长,交AB的延长线于点F,AP、BE相交于点O.下列结论:①EP平分∠CEB;②![]() =PBEF;③PFEF=2
=PBEF;③PFEF=2![]() ;④EFEP=4AOPO.其中正确的是( )
;④EFEP=4AOPO.其中正确的是( )
A. ①②③B. ①②④C. ①③④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
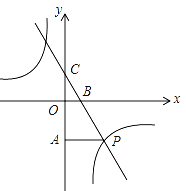
【题目】如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数![]() 的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18.
的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18.
(1)求上述一次函数与反比例函数的表达式;
(2)设Q是一次函数y=kx+3图象上的一点,且满足△OCQ的面积是△BCO面积的2倍,求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
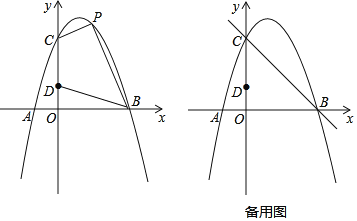
【题目】如图,对称轴为直线x=1的抛物线经过A(﹣1,0)、C(0,3)两点,与x轴的另一个交点为B,点D在y轴上,且OB=3OD
(1)求该抛物线的表达式;
(2)设该抛物线上的一个动点P的横坐标为t
①当0<t<3时,求四边形CDBP的面积S与t的函数关系式,并求出S的最大值;
②点Q在直线BC上,若以CD为边,点C、D、Q、P为顶点的四边形是平行四边形,请求出所有符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
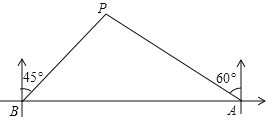
【题目】如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com