
【题目】设a,b,c为互不相等的实数,且满足关系式:b2+c2=2a2+16a+14①bc=a2﹣4a﹣5②.求a的取值范围.
【答案】a的取值范围为a>﹣1且![]() 且
且![]() .
.
【解析】
先通过代数式变形得(b+c)2=2a2+16a+14+2(a2-4a-5)=4a2+8a+4=4(a+1)2,即有b+c=±2(a+1).有了b+c与bc,就可以把b,c可作为一元二次方程x2±2(a+1)x+a2-4a-5=0③的两个不相等实数根,由△=4(a+1)2-4(a2-4a-5)=24a+24>0,得到a>-1.再排除a=b和a=c时的a的值.先设a=b和a=c,分别代入方程③,求得a的值,则题目要求的a的取值范围应该是在a>-1的前提下排除求得的a值.
∵b2+c2=2a2+16a+14,bc=a2﹣4a﹣5,
∴(b+c)2=2a2+16a+14+2(a2﹣4a﹣5)=4a2+8a+4=4(a+1)2,
即有b+c=±2(a+1).
又bc=a2﹣4a﹣5,
所以b,c可作为一元二次方程x2±2(a+1)x+a2﹣4a﹣5=0③的两个不相等实数根,
故△=4(a+1)2﹣4(a2﹣4a﹣5)=24a+24>0,
解得a>﹣1.
若当a=b时,那么a也是方程③的解,
∴a2±2(a+1)a+a2﹣4a﹣5=0,
即4a2﹣2a﹣5=0或﹣6a﹣5=0,
解得,![]() 或
或![]() .
.
当a=c时,同理可得![]() 或
或![]() .
.
所以a的取值范围为a>﹣1且![]() 且
且![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
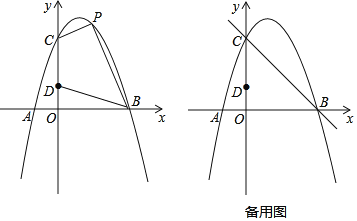
【题目】如图,对称轴为直线x=1的抛物线经过A(﹣1,0)、C(0,3)两点,与x轴的另一个交点为B,点D在y轴上,且OB=3OD
(1)求该抛物线的表达式;
(2)设该抛物线上的一个动点P的横坐标为t
①当0<t<3时,求四边形CDBP的面积S与t的函数关系式,并求出S的最大值;
②点Q在直线BC上,若以CD为边,点C、D、Q、P为顶点的四边形是平行四边形,请求出所有符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
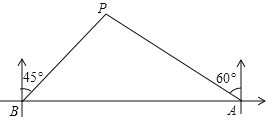
【题目】如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
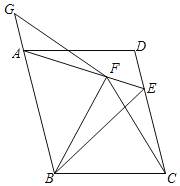
【题目】在平行四边形ABCD中,以AB为边作等边△ABE,点E在CD上,以BC为边作等边△BCF,点F在AE上,点G在BA延长线上且FG=FB.
(1)若CD=6,AF=3,求△ABF的面积;
(2)求证:BE=AG+CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() 是常数)经过点
是常数)经过点![]() .
.
(1)求该抛物线的解析式和顶点坐标;
(2)P(m,t)为抛物线上的一个动点,![]() 关于原点的对称点为
关于原点的对称点为![]() .
.
①当点![]() 落在该抛物线上时,求
落在该抛物线上时,求![]() 的值;
的值;
②当点![]() 落在第二象限内,
落在第二象限内,![]() 取得最小值时,求
取得最小值时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,过点A作直线EF.
(1)如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三种情况).
(ī) (īī) (īīī)
(2)如图(2),若AB为非直径的弦,∠CAE=∠B,则EF是⊙O的切线吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把可以自由转动的圆形转盘A,B分别分成3等份的扇形区域,并在每一个小区域内标上数字.小明和小颖两个人玩转盘游戏,游戏规则是:同时转动两个转盘,当转盘停止时,若指针两区域的数字均为奇数,则小明胜;若指针两区域的数字均为偶数,则小颖胜;若有指针落在分割线上,则无效,需重新转动转盘.这个游戏规则对双方公平吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4![]() ,BC=4,点D是AC的中点,点F是边AB上一动点,沿DF所在直线把△ADF翻折到△A′DF的位置,若线段A′D交AB于点E,且△BA′E为直角三角形,则BF的长为_____.
,BC=4,点D是AC的中点,点F是边AB上一动点,沿DF所在直线把△ADF翻折到△A′DF的位置,若线段A′D交AB于点E,且△BA′E为直角三角形,则BF的长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com