（本题满分8分）如图在△AFD和△CEB中，点A，E，F，C在同一条直线上，有下面四个论断：
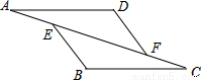
（1）AD=CB，（2）AE=CF，（3）∠B=∠D，（4）AD∥BC．请你从中选三个作为题设，余下的一个作为结论，写出一个正确的命题，并加以证明．
科目：初中数学 来源：2014-2015学年江苏省无锡市锡北片七年级下学期期中考试数学试卷（解析版） 题型：填空题
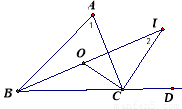
△ABC中, ∠ABC=40°，∠ACB=80°，BO、CO分别平分∠ABC，∠ACB，交于O，CI为外角∠ACD的平分线，BO的延长线交CI于I点，记∠BAC=∠1，∠BIC=∠2，则∠1：∠2= （求比值）．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年湖北省七年级5月联考数学试卷（解析版） 题型：解答题
（12分）在平面直角坐标系中，有一点B（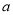
，
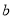）的横纵坐标满足条件：
．
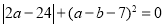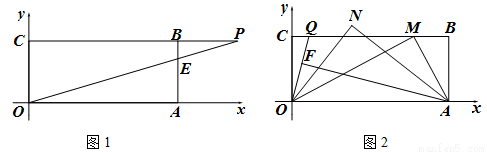
（1）（3分）求点B的坐标。
（2）（4分）如图1，过点B作BA⊥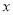
轴于A，BC⊥
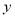轴于C，P为CB延长线上一点，OP交BA于E，若
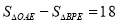，求P、E两点坐标。
（3）（5分）M为（2）中BC上一点，如图2，且OM⊥AM，Q为CM上一动点，F为OQ上一动点，∠FAO=∠COQ，ON、AN分别平分∠QOM与∠FAM，当Q点运动时，∠N变化吗？若不变，求其值；若变化，说明理由。
查看答案和解析>>
科目：初中数学 来源：2014-2015学年湖北省七年级5月联考数学试卷（解析版） 题型：选择题
将一直角三角板与两边平行的纸条如图所示放置，若∠1=2∠2，则∠3的度数是（ ）
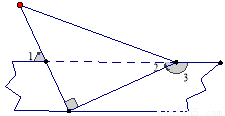
A、100° B、120° C、130° D、150°
查看答案和解析>>
科目：初中数学 来源：2014-2015学年湖北省黄冈市罗田县八年级上学期期中联考数学试卷（解析版） 题型：填空题
（本题满分12分）已知△ABC中，AC=BC，∠ACB=90゜，点P在射线AC上，连接PB，将线段PB绕点B逆时针旋转90゜得线段BN，AN交直线BC于M．
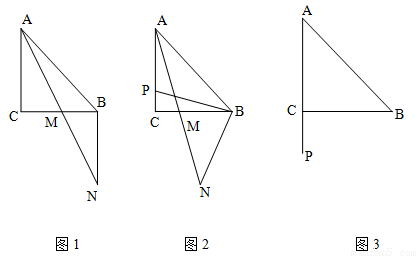
（1）如图1．若点P与点C重合，则AM ：MN = ； MC ：AP= （直接写出结果）：
（2）如图2，若点P在线段AC上，求证：AP=2MC；
（3）如图3，若点P在线段AC的延长线上，完成图形，并直接写出MC ：AP =
查看答案和解析>>
科目：初中数学 来源：2014-2015学年湖北省黄冈市罗田县八年级上学期期中联考数学试卷（解析版） 题型：填空题
如图，在△ABC中，AB=8，BC=6，AC的垂直平分线MN交AB，AC于点M，N．则△BCM的周长为 ．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年湖北省黄冈市罗田县八年级上学期期中联考数学试卷（解析版） 题型：选择题
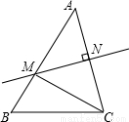
如图，△ABC中，D是BC中点，DE⊥DF，E、F分别在AB、AC上，则BE+CF（ ）
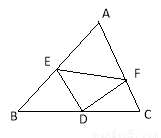
A．大于EF B．等于EF C．小于EF D．与EF的大小无法确定
查看答案和解析>>
科目：初中数学 来源：2014-2015学年重庆市九年级第三次模拟考试数学试卷（解析版） 题型：填空题
有7张正面分别标有数字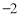
，
，0，1，2，3，4的卡片，除数字不同外其余全部相同，现将它们背面朝上，洗匀后从中随机抽取一张，记卡片上的数字为m，则使关于x的方程
有实数根，且使不等式组
无解的概率是 ．
查看答案和解析>>
科目：初中数学 来源：2015年初中毕业升学考试（浙江衢州卷）数学（解析版） 题型：解答题
小明在课外学习时遇到这样一个问题：
定义：如果二次函数y=a1x2+b1x+c1（a1≠0，a1，b1，c1是常数）与y=a2x2+b2x+c2（a2≠0，a2，b2，c2是常数）满足a1+a2=0，b1=b2，c1+c2=0，则称这两个函数互为“旋转函数”．
求函数y=﹣x2+3x﹣2的“旋转函数”．
小明是这样思考的：由函数y=﹣x2+3x﹣2可知，a1=﹣1，b1=3，c1=﹣2，根据a1+a2=0，b1=b2，c1+c2=0，求出a2，b2，c2，就能确定这个函数的“旋转函数”．
请参考小明的方法解决下面问题：
（1）写出函数y=﹣x2+3x﹣2的“旋转函数”；
（2）若函数y=﹣x2+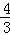
mx﹣2与y=x2﹣2nx+n互为“旋转函数”，求（m+n）2015的值；
（3）已知函数y=﹣
（x+1）（x﹣4）的图象与x轴交于点A、B两点，与y轴交于点C，点A、B、C关于原点的对称点分布是A1，B1，C1，试证明经过点A1，B1，C1的二次函数与函数y=﹣
（x+1）（x﹣4）互为“旋转函数．”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
