
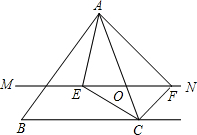
 △ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠DCA的平分线于点F.
△ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠DCA的平分线于点F.分析 (1)由于CE平分∠BCA,那么有∠1=∠2,而MN∥BC,利用平行线的性质有∠1=∠3,等量代换有∠2=∠3,于OE=OC,同理OC=OF,于是OE=OF;
(2)OA=OC,那么可证四边形AECF是平行四边形,又CE、CF分别是∠BCA及其外角的角平分线,易证∠ECF是90°,从而可证四边形AECF是矩形.
解答 (1)解:当点O运动到AC中点时,四边形AECF是矩形;理由如下: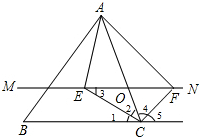 如图所示:
如图所示:
∵CE平分∠BCA,
∴∠1=∠2,
又∵MN∥BC,
∴∠1=∠3,
∴∠3=∠2,
∴EO=CO,
同理,FO=CO,
∴EO=FO;
(2)解:∵OA=OC,
∴四边形AECF是平行四边形,
∵CF是∠BCA的外角平分线,
∴∠4=∠5,
又∵∠1=∠2,
∴∠1+∠5=∠2+∠4,
又∵∠1+∠5+∠2+∠4=180°,
∴∠2+∠4=90°,
∴平行四边形AECF是矩形.
点评 本题考查了矩形判定,平行四边形判定,平行线性质,角平分线定义的应用,主要考查学生的推理能力.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:解答题
 如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示的数为-$\sqrt{2}$,设点B所表示的数为n.
如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示的数为-$\sqrt{2}$,设点B所表示的数为n.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
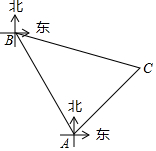 黄岩岛自古以来就是中国的领土,如图,为维护海洋利益,三沙市一艘海监船在黄岩岛附近海域巡航,某一时刻海监船在A处测得该岛上某一目标C在它的北偏东45°方向,海监船以30海里每小时的速度沿北偏西30°方向航行2小时后到达B处,此时测得该目标C在它的南偏东75°方向.求:
黄岩岛自古以来就是中国的领土,如图,为维护海洋利益,三沙市一艘海监船在黄岩岛附近海域巡航,某一时刻海监船在A处测得该岛上某一目标C在它的北偏东45°方向,海监船以30海里每小时的速度沿北偏西30°方向航行2小时后到达B处,此时测得该目标C在它的南偏东75°方向.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)解方程组$\left\{\begin{array}{l}x+2y=5\\ x+y=2.\end{array}$
(1)解方程组$\left\{\begin{array}{l}x+2y=5\\ x+y=2.\end{array}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
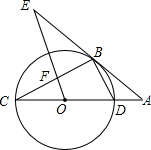 如图所示,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AB于点E.
如图所示,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AB于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com