
【题目】如图,AB是⊙O的直径,弦AD平分∠BAC,DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AD=BC,⊙O半径为6,求∠CAD与![]() 围成的阴影部分的面积.
围成的阴影部分的面积.
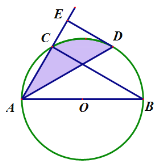
【答案】(1)直线DE与⊙O相切,理由见解析;(2)6![]()
【解析】
(1)连接OD,由AD为角平分线,得到一对角相等,再由OA=OD,得到一对角相等,通过等量代换得到一对内错角相等;根据上步结论可推理得到平行线,再结合AE⊥ED即可证得结论;
(2)先判断△COD是等边三角形,根据等底同高的三角形的面积相等可知S△ACD=S△COD,从而∠CAD与弧CD围成的阴影部分的面积=扇形COD的面积.
解:(1)直线DE与⊙O相切,
理由如下:连接OD,如图所示:
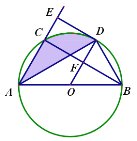
∵AD平分∠BAC,
∴∠EAD=∠OAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠ODA=∠EAD,
∴EA∥OD,
∵DE⊥EA,
∴DE⊥OD,
又∵点D在⊙O上,
∴直线DE与⊙O相切;
(2)连接CD,OC.
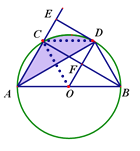
∵AD=BC,
∴ 弧AD =弧BC ,
∴ 弧AC = 弧BD ,
∵ 弧CD = 弧BD ,
∴ 弧AC = 弧CD =弧BD,
∴∠COD=∠BOD=60°,
∵OC=OD,
∴△COD是等边三角形,
∴∠CDO=∠DOB=60°,
∴CD∥AB,
∴S△ACD=S△COD,
∴∠CAD与弧CD围成的阴影部分的面积=扇形COD的面积=![]() .
.


科目:初中数学 来源: 题型:
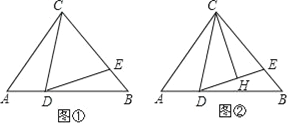
【题目】如图在等腰三角形△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.
(1)如图①,若BC=BD,求证:CD=DE;
(2)如图②,过点C作CH⊥DE,垂足为H,若CD=BD,EH=1,求DE﹣BE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
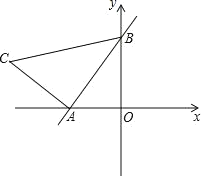
【题目】如图,直线y=kx+2与x轴、y轴分别交于A、B两点,OA:OB=![]() .以线段AB为边在第二象限内作等腰Rt△ABC,∠BAC=90°.
.以线段AB为边在第二象限内作等腰Rt△ABC,∠BAC=90°.
(1)求点A的坐标和k的值;
(2)求点C坐标;
(3)直线y=![]() x在第一象限内的图象上是否存在点P,使得△ABP的面积与△ABC的面积相等?如果存在,求出点P坐标;如果不存在,请说明理由.
x在第一象限内的图象上是否存在点P,使得△ABP的面积与△ABC的面积相等?如果存在,求出点P坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
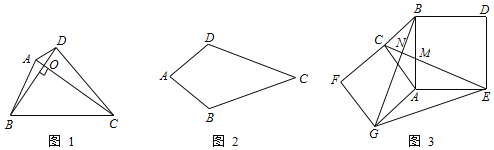
【题目】阅读理解:如图1,若一个四边形的两条对角线互相垂直,则称这个四边形为垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;
(2)性质探究:如图1,试在垂美四边形ABCD中探究AB2,CD2,AD2,BC2之间的关系,并说明理由;
(3)解决问题:如图3,分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE、CE交BG于点N,交AB于点M.已知AC=![]() ,AB=2,求GE的长.
,AB=2,求GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的发展,油电混合动力汽车已经开始普及,某种型号油电混合动力汽车,从甲地到乙地燃油行驶纯燃油费用80元,从甲地到乙地用电行驶纯电费用30元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元
(1)求每行驶1千米纯用电的费用;
(2)若要使从甲地到乙地油电混合行驶所需的油、电费用合计不超过50元,则至多用纯燃油行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
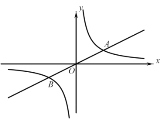
【题目】已知点A(2,1)是正比例函数ykx(其中k0)和反比例函数y![]() (其中t0)的图像在第一象限的交点,点B是这两个函数图像的另一个交点,点C是x轴上一点.
(其中t0)的图像在第一象限的交点,点B是这两个函数图像的另一个交点,点C是x轴上一点.
(1)求这两个函数的解析式并直接写出点B的坐标;
(2)求当ABC为等腰三角形时,点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图1,将一张直角三角形纸片ABC折叠,使点A与点C重合,这时DE为折痕,△CBE为等腰三角形;再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.

(1)如图2,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图2中画出折痕;
(2)如图3,在正方形网格中,以给定的BC为一边,画出一个斜三角形ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形;
(3)如果一个三角形所折成的“叠加矩形”为正方形,那么它必须满足的条件是 ;
(4)如果一个四边形一定能折成“叠加矩形”,那么它必须满足的条件是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 移动,同时点
移动,同时点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 的延长线移动,点
的延长线移动,点![]() ,
,![]() 移动的速度相同,
移动的速度相同,![]() 与
与![]() 相交于点
相交于点![]() .
.
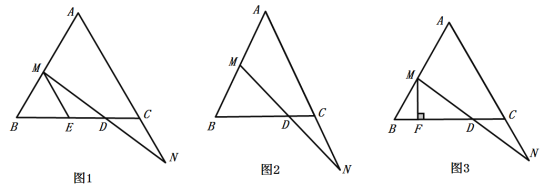
(1)如图1,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(2)如图2,![]() ,当点
,当点![]() 移动到
移动到![]() 的中点时,求
的中点时,求![]() 的长度;
的长度;
(3)如图3,过点![]() 作
作![]() 于点
于点![]() .在点
.在点![]() 从点
从点![]() 向点
向点![]() (点
(点![]() 不与点
不与点![]() ,
,![]() 重合)移动的过程中,线段
重合)移动的过程中,线段![]() 与
与![]() 的长度是否保持不变若保持不变,请求出
的长度是否保持不变若保持不变,请求出![]() 与
与![]() 的长度和;若改变,请说明理由.
的长度和;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书测算,有如下方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用6天;
(3)若甲、乙两队合作3天,余下的工程由乙队单独做也正好如期完成.
试问:(1)规定日期是多少天?
(2)在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com