
【题目】将图1,将一张直角三角形纸片ABC折叠,使点A与点C重合,这时DE为折痕,△CBE为等腰三角形;再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.

(1)如图2,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图2中画出折痕;
(2)如图3,在正方形网格中,以给定的BC为一边,画出一个斜三角形ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形;
(3)如果一个三角形所折成的“叠加矩形”为正方形,那么它必须满足的条件是 ;
(4)如果一个四边形一定能折成“叠加矩形”,那么它必须满足的条件是 .
科目:初中数学 来源: 题型:
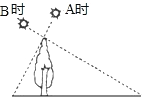
【题目】如图,在 A 时测得某树(垂直于地面)的影长为 4 米,B 时又测得该树的影长为 16 米,若两次日 照的光线互相垂直,则树的高度为_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】酒泉市教育局计划对全市八年级学生学习情况进行调查,随机从全市抽取城市和农村两组学生的期中数学成绩,每组10人进行对比分析.绘制统计图如下.根据图中信息,完成下列问题.
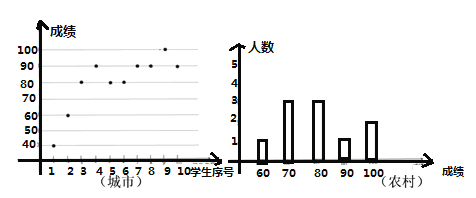
(1)完成下表;
平均数 | 中位数 | 众数 | 方差 | |
城市 | ||||
农村 |
(2)依据上表的信息谈谈你的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
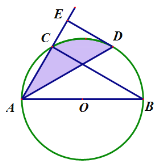
【题目】如图,AB是⊙O的直径,弦AD平分∠BAC,DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AD=BC,⊙O半径为6,求∠CAD与![]() 围成的阴影部分的面积.
围成的阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种成本为每千克![]() 元的水产品,据市场分析,若按每千克
元的水产品,据市场分析,若按每千克![]() 元销售,一个月能售出
元销售,一个月能售出![]() ,销售单价每涨(或跌)
,销售单价每涨(或跌)![]() 元,月销售量就减少(或增加)
元,月销售量就减少(或增加)![]() ,解答以下问题:
,解答以下问题:
(1)当销售单价定位每千克![]() 元时,计算月销售量和月销售利润;
元时,计算月销售量和月销售利润;
(2)商店想在月销售成本不超过![]() 元的情况下,使得月销售利润达到
元的情况下,使得月销售利润达到![]() 元,销售单价应为多少?
元,销售单价应为多少?
(3)商店要使得月销售利润达到最大,销售单价应为多少?此时利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(![]() ,
,![]() )
)
B. 当m>0时,函数图象截x轴所得的线段长度大于![]()
C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>![]() 时,y随x的增大而减小
时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.
(1)求平均每次下调的百分率;
(2)某人准备以开盘均价购买一套100平方米的房子,开发商给予以下两种优惠方案供其选择:①打9.8折销售;②不打折,送两年物业管理费.物业管理费每平方米每月1.5元,请问哪种方案更优惠?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com