
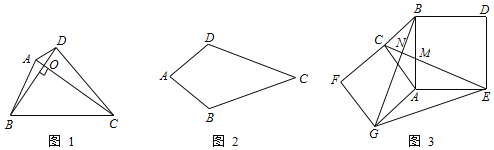
【题目】阅读理解:如图1,若一个四边形的两条对角线互相垂直,则称这个四边形为垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;
(2)性质探究:如图1,试在垂美四边形ABCD中探究AB2,CD2,AD2,BC2之间的关系,并说明理由;
(3)解决问题:如图3,分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE、CE交BG于点N,交AB于点M.已知AC=![]() ,AB=2,求GE的长.
,AB=2,求GE的长.
【答案】(1)四边形ABCD是垂直四边形,理由见解析;(2)AB2+CD2=AD2+BC2,见解析;(3)![]()
【解析】
(1)由题意直接根据垂直平分线的判定定理证明即可;
(2)由题意直接根据垂直的定义和勾股定理解答即可;
(3)由题意根据垂美四边形的性质、勾股定理、结合(2)的结论计算.
解:(1)如图2,四边形ABCD是垂直四边形;
理由如下:
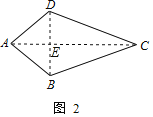
连接AC、BD交于点E,
∵AB=AD,
∴点A在线段BD的垂直平分线上,
∵CB=CD,
∴点C在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,
∴AC⊥BD,即四边形ABCD是垂美四边形;
(2)猜想结论:AB2+CD2=AD2+BC2,
证明:如图1,在四边形ABCD中,
∵AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得:AB2+CD2=AO2+BO2+OD2+OC2AD2+BC2=AO2+BO2+OD2+OC2
∴AB2+CD2=AD2+BC2,
(3)如图3,连接CG,BE,
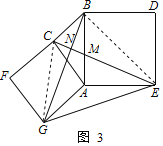
∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
在△GAB和△CAE中,
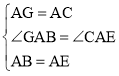
∴△GAB≌△CAE(SSS),
∴∠ABG=∠AEC,
∵∠AEC+∠AME=90°,
∴∠ABG+∠BMN=90°,
∴∠BNC=90°,即BG⊥CE,
∴四边形CGEB是垂美四边形,
由(2)得:EG2+BC2=CG2+BE2
∵![]() ,AB=2,
,AB=2,
∴BC=1,![]() ,
,![]() ,
,
∴EG2=CG2+BE2﹣BC2=6+8﹣2=13,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() ,求证:
,求证:![]() .
.

(2)类比探究:如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,![]() 点在边
点在边![]() 的延长线上,连接
的延长线上,连接![]() .请判断:①
.请判断:①![]() 的度数为_________.②线段
的度数为_________.②线段![]() 之间的数量关系是_________.
之间的数量关系是_________.
(3)问题解决:在(2)中,如果![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在![]() 地时距地面的高度
地时距地面的高度![]() 为 米;
为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式.
(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保障北京2022 年冬季奥运会赛场间的交通服务,北京将建设连接北京城区-延庆区-崇礼县三地的高速铁路和高速公路.在高速公路方面,目前主要的交通方式是通过京藏高速公路(G6),其路程为220公里.为将崇礼县纳入北京一小时交通圈,有望新建一条高速公路,将北京城区到崇礼的道路长度缩短到100公里.如果行驶的平均速度每小时比原来快22公里,那么从新建高速行驶全程所需时间与从原高速行驶全程所需时间比为4:11.求从新建高速公路行驶全程需要多少小时?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】酒泉市教育局计划对全市八年级学生学习情况进行调查,随机从全市抽取城市和农村两组学生的期中数学成绩,每组10人进行对比分析.绘制统计图如下.根据图中信息,完成下列问题.
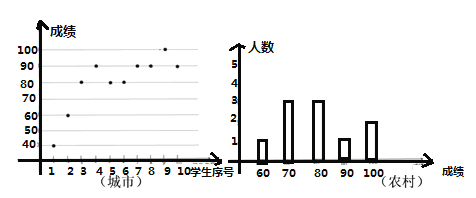
(1)完成下表;
平均数 | 中位数 | 众数 | 方差 | |
城市 | ||||
农村 |
(2)依据上表的信息谈谈你的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 | 方差 |
八(1) | 85 | b | c | 22.8 |
八(2) | a | 85 | 85 | 19.2 |
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
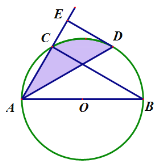
【题目】如图,AB是⊙O的直径,弦AD平分∠BAC,DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AD=BC,⊙O半径为6,求∠CAD与![]() 围成的阴影部分的面积.
围成的阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种成本为每千克![]() 元的水产品,据市场分析,若按每千克
元的水产品,据市场分析,若按每千克![]() 元销售,一个月能售出
元销售,一个月能售出![]() ,销售单价每涨(或跌)
,销售单价每涨(或跌)![]() 元,月销售量就减少(或增加)
元,月销售量就减少(或增加)![]() ,解答以下问题:
,解答以下问题:
(1)当销售单价定位每千克![]() 元时,计算月销售量和月销售利润;
元时,计算月销售量和月销售利润;
(2)商店想在月销售成本不超过![]() 元的情况下,使得月销售利润达到
元的情况下,使得月销售利润达到![]() 元,销售单价应为多少?
元,销售单价应为多少?
(3)商店要使得月销售利润达到最大,销售单价应为多少?此时利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
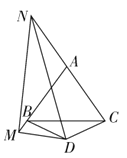
【题目】如图,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,M是AB延长线上一点,N是CA延长线上一点,且∠MDN=60°.试探BM,MN,CN之间的数量关系,并给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com