
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在![]() 地时距地面的高度
地时距地面的高度![]() 为 米;
为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式.
(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?

【答案】(1)10;30;(2)![]() ;(3)4分钟、9分钟或15分钟.
;(3)4分钟、9分钟或15分钟.
【解析】
(1)根据速度=高度÷时间即可算出甲登山上升的速度;根据高度=速度×时间即可算出乙在A地时距地面的高度b的值;
(2)分0≤x≤2和x≥2两种情况,根据高度=初始高度+速度×时间即可得出y关于x的函数关系;
(3)当乙未到终点时,找出甲登山全程中y关于x的函数关系式,令二者做差等于50即可得出关于x的一元一次方程,解之即可求出x值;当乙到达终点时,用终点的高度-甲登山全程中y关于x的函数关系式=50,即可得出关于x的一元一次方程,解之可求出x值.综上即可得出结论.
(1)(300-100)÷20=10(米/分钟),
b=15÷1×2=30.
故答案为:10;30.
(2)当0≤x≤2时,y=15x;
当x≥2时,y=30+10×3(x-2)=30x-30.
当y=30x-30=300时,x=11.
∴乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为![]() .
.
(3)甲登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=10x+100(0≤x≤20).
当10x+100-(30x-30)=50时,解得:x=4;
当30x-30-(10x+100)=50时,解得:x=9;
当300-(10x+100)=50时,解得:x=15.
答:登山4分钟、9分钟或15分钟时,甲、乙两人距地面的高度差为50米.


科目:初中数学 来源: 题型:
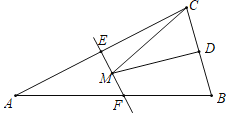
【题目】如图,等腰三角形ABC的底边BC长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM的周长的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
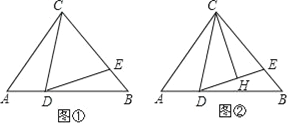
【题目】如图在等腰三角形△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.
(1)如图①,若BC=BD,求证:CD=DE;
(2)如图②,过点C作CH⊥DE,垂足为H,若CD=BD,EH=1,求DE﹣BE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
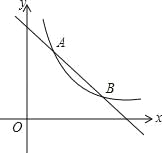
【题目】如图,一次函数 y=﹣x+4 的图象与反比例 y=![]() (k 为常数, 且 k≠0)的图象交于 A(1,a)、B(b,1)两点.
(k 为常数, 且 k≠0)的图象交于 A(1,a)、B(b,1)两点.
(1)求点 A、B 的坐标及反比例函数的表达式;
(2)在 x 轴上找一点,使 PA+PB 的值最小,求满足条件的点 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
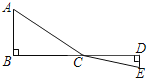
【题目】如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=8,设CD=x.
(1)用含x的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小;
(3)根据(2)中的规律和结论,请构图求出代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
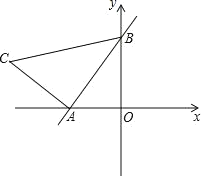
【题目】如图,直线y=kx+2与x轴、y轴分别交于A、B两点,OA:OB=![]() .以线段AB为边在第二象限内作等腰Rt△ABC,∠BAC=90°.
.以线段AB为边在第二象限内作等腰Rt△ABC,∠BAC=90°.
(1)求点A的坐标和k的值;
(2)求点C坐标;
(3)直线y=![]() x在第一象限内的图象上是否存在点P,使得△ABP的面积与△ABC的面积相等?如果存在,求出点P坐标;如果不存在,请说明理由.
x在第一象限内的图象上是否存在点P,使得△ABP的面积与△ABC的面积相等?如果存在,求出点P坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
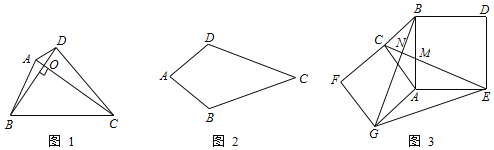
【题目】阅读理解:如图1,若一个四边形的两条对角线互相垂直,则称这个四边形为垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;
(2)性质探究:如图1,试在垂美四边形ABCD中探究AB2,CD2,AD2,BC2之间的关系,并说明理由;
(3)解决问题:如图3,分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE、CE交BG于点N,交AB于点M.已知AC=![]() ,AB=2,求GE的长.
,AB=2,求GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 移动,同时点
移动,同时点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 的延长线移动,点
的延长线移动,点![]() ,
,![]() 移动的速度相同,
移动的速度相同,![]() 与
与![]() 相交于点
相交于点![]() .
.
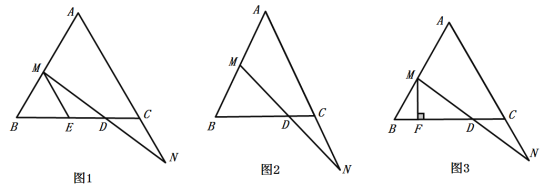
(1)如图1,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(2)如图2,![]() ,当点
,当点![]() 移动到
移动到![]() 的中点时,求
的中点时,求![]() 的长度;
的长度;
(3)如图3,过点![]() 作
作![]() 于点
于点![]() .在点
.在点![]() 从点
从点![]() 向点
向点![]() (点
(点![]() 不与点
不与点![]() ,
,![]() 重合)移动的过程中,线段
重合)移动的过程中,线段![]() 与
与![]() 的长度是否保持不变若保持不变,请求出
的长度是否保持不变若保持不变,请求出![]() 与
与![]() 的长度和;若改变,请说明理由.
的长度和;若改变,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com