
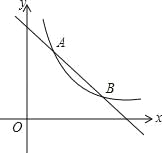
【题目】如图,一次函数 y=﹣x+4 的图象与反比例 y=![]() (k 为常数, 且 k≠0)的图象交于 A(1,a)、B(b,1)两点.
(k 为常数, 且 k≠0)的图象交于 A(1,a)、B(b,1)两点.
(1)求点 A、B 的坐标及反比例函数的表达式;
(2)在 x 轴上找一点,使 PA+PB 的值最小,求满足条件的点 P 的坐标.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)将x=1代入直线AB的函数表达式中即可求出点A的坐标,由点A的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数的表达式,联立两函数表达式成方程组,通过解方程组即可求出点B的坐标;
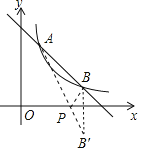
(2)作B点关于x轴的对称点B′(2,-1),连接AB’,交x轴于点P,连接PB,由两点之间线段最短可得出此时PA+PB取最小值,根据点A、B′的坐标利用待定系数法可求出直线AB′的函数表达式,再利用一次函数图象上点的坐标特征即可求出点P的坐标.
![]() 在一次函数
在一次函数![]() 的图象上,
的图象上,
![]() ,
,
![]() .
.
![]() 在反比例
在反比例![]() 为常数,且
为常数,且![]() 的图象上,
的图象上,
![]() ,
,
![]() 反比例函数的表达式为
反比例函数的表达式为![]() .
.
联立一次函数与反比例函数关系式成方程组,得:
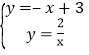 ,解得:
,解得:![]() ,
,
![]() .
.
![]() 作B点关于x轴的对称点
作B点关于x轴的对称点![]() ,连接
,连接![]() ,交x轴于点P,连接PB,如图所示.
,交x轴于点P,连接PB,如图所示.
![]() 点B、
点B、![]() 关于x轴对称,
关于x轴对称,
![]() .
.
![]() 点A、P、
点A、P、![]() 三点共线,
三点共线,
![]() 此时
此时![]() 取最小值.
取最小值.
设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
将![]() 代入
代入![]() ,
,
![]() ,解得:
,解得:![]() ,
,
![]() 直线
直线![]() 的函数表达式为
的函数表达式为![]() .
.
当![]() 时,
时,![]() ,
,
![]() 满足条件的点P的坐标为
满足条件的点P的坐标为![]() .
.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】探索与证明:
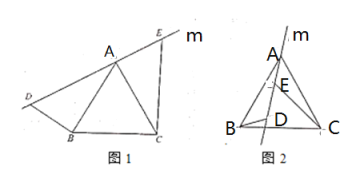
(1)如图1,直线![]() 经过正三角形
经过正三角形![]() 的项点
的项点![]() ,在直线
,在直线![]() 上取两点
上取两点![]() ,
,![]() ,使得
,使得![]() ,
,![]() .通过观察或测量,猜想线段
.通过观察或测量,猜想线段![]() ,
,![]() 与
与![]() 之间满足的数量关系,并子以证明:
之间满足的数量关系,并子以证明:
(2)将(1)中的直线![]() 绕着点
绕着点![]() 逆时针方向旋转一个角度到如图2的位置,并使
逆时针方向旋转一个角度到如图2的位置,并使![]() ,
,![]() .通过观察或测量,猜想线段
.通过观察或测量,猜想线段![]() ,
,![]() 与
与![]() 之间满足的数量关系,并予以证明.
之间满足的数量关系,并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
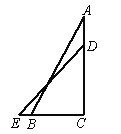
【题目】如图,将一幅三角板的直角顶点重合放置,其中∠A=30°,∠CDE=45°.若三角板ACB的位置保持不动,将三角板DCE绕其直角顶点C顺时针旋转一周.若△DCE其中一边与AB平行,则∠ECB的度数为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
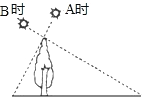
【题目】如图,在 A 时测得某树(垂直于地面)的影长为 4 米,B 时又测得该树的影长为 16 米,若两次日 照的光线互相垂直,则树的高度为_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从![]() 两地同时出发,沿同一公路相向而行,开往
两地同时出发,沿同一公路相向而行,开往![]() 两地.已知甲车每小时比乙车每小时多走
两地.已知甲车每小时比乙车每小时多走![]() ,且甲车行驶
,且甲车行驶![]() 所用的时间与乙车行驶
所用的时间与乙车行驶![]() 所用的时间相同.
所用的时间相同.
(1)求甲、乙两车的速度各是多少![]() ?
?
(2)实际上,甲车出发后,在途中因车辆故障耽搁了20分钟,但仍比乙车提前1小时到达目的地.求![]() 两地间的路程是多少
两地间的路程是多少![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在![]() 地时距地面的高度
地时距地面的高度![]() 为 米;
为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式.
(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在![]() 地时距地面的高度
地时距地面的高度![]() 为 米;
为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式.
(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】酒泉市教育局计划对全市八年级学生学习情况进行调查,随机从全市抽取城市和农村两组学生的期中数学成绩,每组10人进行对比分析.绘制统计图如下.根据图中信息,完成下列问题.
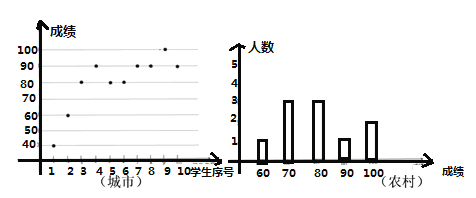
(1)完成下表;
平均数 | 中位数 | 众数 | 方差 | |
城市 | ||||
农村 |
(2)依据上表的信息谈谈你的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(![]() ,
,![]() )
)
B. 当m>0时,函数图象截x轴所得的线段长度大于![]()
C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>![]() 时,y随x的增大而减小
时,y随x的增大而减小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com