
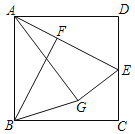
【题目】如图,在正方形ABCD中,E是CD边上一点,DE=2,过B作AE的垂线,垂足为点F,BF=3,将△ADE沿AE翻折,得到△AGE,AG与BF于点M,连接BG,则△BMG的周长为______
【答案】![]()
【解析】
延长BF交AD于K,作BH⊥AG于H.首先证明AK=DE=2,再利用相似三角形的性质求出FK,再证明∠ABK=30°,把问题特殊化后即可解决问题.
如图,延长BF交AD于K,作BH⊥AG于H.

∵四边形ABCD是正方形,
∴AB=AD,∠BAK=∠ADE=90°,
∵BF⊥AE,
∴∠AFB=90°,
∴∠BAF+∠ABF=90°,∠BAF+∠DAE=90°,
∴∠ABK=∠DAE,
∴△ABK≌△ADE(ASA),
∴AK=DE=2,
∵∠AKF=∠AKB,∠AFK=∠KAB=90°,
∴△AKF∽△BKA,
∴![]() =
=![]() ,设KF=x,
,设KF=x,
则有![]() =
=![]() ,
,
整理得![]() ,
,
解得x=1或﹣4(舍弃),
∴BK=BF+FK=3+1=4,
∵sin∠ABK=![]() =
=![]() =
=![]() ,
,
∴∠ABK=30°,
∴∠DAE=∠ABK=∠EAG=∠BAG=30°,
∴MA=MB,
在Rt△ABH中,∵AB=2![]() ,∠BAH=30°,∠AHB=90°,
,∠BAH=30°,∠AHB=90°,
∴BH=![]() AB=
AB=![]() ,AH=
,AH=![]() BH=3,
BH=3,
∵AD=AB=AG=2![]() ,
,
∴HG=2![]() ﹣3,
﹣3,
∴BG=![]() =
=![]() =3
=3![]() ﹣
﹣![]() ,
,
∴△BMG的周长=BM+GM+BG=AM+GM+BG=AG+BG=2![]() +3
+3![]() ﹣
﹣![]() .
.
故答案为:![]() .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC-CB运动,到点B停止.过点P作PD⊥AB,垂足为D,PD的长y(cm)与点P的运动时间x(秒)的函数图象如图2所示.当点P运动5秒时,PD的长是( )
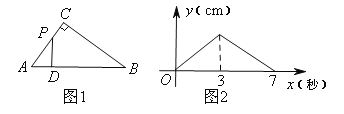
A.1.5cmB.1.2cmC.1.8cmD.2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
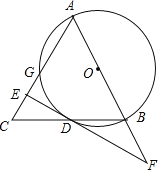
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点G,过D作EF⊥AC于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)当∠BAC=60°,AB=8时,求EG的长;
(3)当AB=5,BC=6时,求tanF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是半圆O的直径,AC是弦,点P沿BA方向,从点B运动到点A,速度为1cm/s,若AB=10cm,点O到AC的距离为4cm.
(1)求弦AC的长;
(2)问经过多长时间后,△APC是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
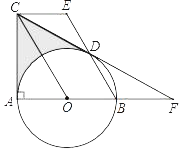
【题目】如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若∠F=30°,EB=8,求图中阴影部分的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知y是x(x>0)的函数,表1中给出了几组x与y的对应值:
表1:
x | … |
| 1 |
| 2 |
| 3 | … |
y | … | 6 | 3 | 2 |
|
| 1 | … |
⑴以表中各对对应值为坐标,在图1的直角坐标系中描出各点,用光滑曲线顺次连接.由图像知,它是我们已经学过的哪类函数?求出函数解析式,并直接写出![]() 的值;
的值;
⑵如果一次函数图像与⑴中图像交于(1,3)和(3,1)两点,在第一、四象限内当x在什么范围时,一次函数的值小于⑴中函数的值?请直接写出答案.

查看答案和解析>>
科目:初中数学 来源: 题型:
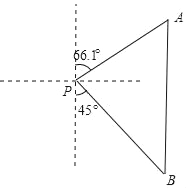
【题目】如图,一艘海轮位于灯塔P的北偏东66.1°方向,距离灯塔120海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,求BP和BA的长(结果取整数).
参考数据:sin66.1°≈0.91,cos66.1°≈0.41,tan64°≈2.26,![]() 取1.414.
取1.414.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解初一年级学生每学期参加综合实践活动的情况,某区教育行政部门随机抽样调查了部分初一学生一个学期参加综合实践活动的天数,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
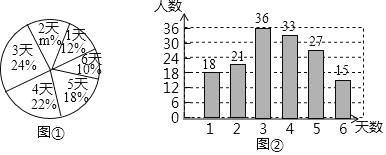
(I)本次随机抽样调查的学生人数为 ,图①中的m的值为 ;
(II)求本次抽样调查获取的样本数据的众数、中位数和平均数;
(III)若该区初一年级共有学生2500人,请估计该区初一年级这个学期参加综合实践活动的天数大于4天的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题探究)如图1,![]() ,直线
,直线![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 到直线
到直线![]() 的距离为2,点
的距离为2,点![]() 到
到![]() 的距离为1,
的距离为1,![]() ,
,![]() ,则
,则![]() 的最小值是______;(提示:将线段
的最小值是______;(提示:将线段![]() 沿
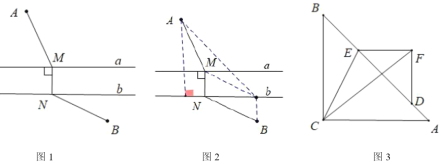
沿![]() 方向平移1个单位长度即可解决,如图2所示.)
方向平移1个单位长度即可解决,如图2所示.)
(关联运用)如图3,在等腰![]() 和等腰
和等腰![]() 中,
中,![]() ,
,![]() 在直线
在直线![]() 上,
上,![]() ,连接
,连接![]() 、
、![]() ,则
,则![]() 的最小值是______.
的最小值是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com