
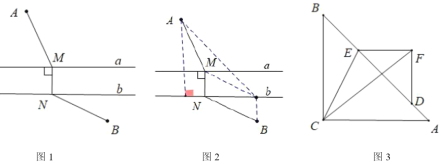
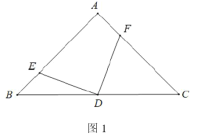
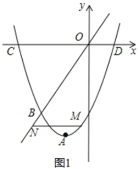
【题目】(问题探究)如图1,![]() ,直线
,直线![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 到直线
到直线![]() 的距离为2,点
的距离为2,点![]() 到
到![]() 的距离为1,
的距离为1,![]() ,
,![]() ,则
,则![]() 的最小值是______;(提示:将线段
的最小值是______;(提示:将线段![]() 沿
沿![]() 方向平移1个单位长度即可解决,如图2所示.)
方向平移1个单位长度即可解决,如图2所示.)
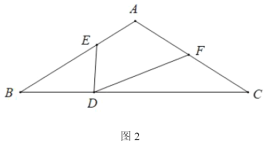
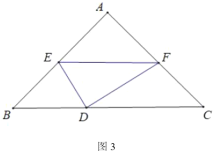
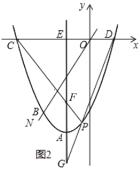
(关联运用)如图3,在等腰![]() 和等腰
和等腰![]() 中,
中,![]() ,
,![]() 在直线
在直线![]() 上,
上,![]() ,连接
,连接![]() 、
、![]() ,则
,则![]() 的最小值是______.
的最小值是______.
【答案】![]()
![]()
【解析】
[问题探究]过点A作AH⊥b于H,过点B作BK⊥b于K,作BJ⊥AH交AH的延长线于J,连接MK、AB和AK,根据两点之间线段最短可得![]() =AM+MK≥AK(当且仅当A、M、K共线时,取等号),然后利用勾股定理求出AK即可;
=AM+MK≥AK(当且仅当A、M、K共线时,取等号),然后利用勾股定理求出AK即可;
[关联运用]过点F作直线l∥BA,交CA的延长线于点N,取AC的中点G,作C关于直线l的对称点M,连接MF、GF、MN,根据对称性和平行四边形的判定及性质推出CF=MF,GF=CE,根据两点之间线段最短可得![]() =GF+MF≥MG(当且仅当G、F、M共线时,取等号),然后利用勾股定理求出MG即可.
=GF+MF≥MG(当且仅当G、F、M共线时,取等号),然后利用勾股定理求出MG即可.
解:[问题探究]过点A作AH⊥b于H,过点B作BK⊥b于K,作BJ⊥AH交AH的延长线于J,连接MK、AB和AK

由图易知,四边形HJBK为矩形,MN=BK=1,MN∥BK,AH=2+1=3,AJ=2+1+1=4
∴四边形MNBK为平行四边形,HK=BJ
∴BN=MK
∴![]() =AM+MK≥AK(当且仅当A、M、K共线时,取等号)
=AM+MK≥AK(当且仅当A、M、K共线时,取等号)
在Rt△ABJ中,BJ=![]()
∴HK=3
∴AK=![]()
∴![]() ≥
≥![]()
即![]() 的最小值是
的最小值是![]() ;
;
故答案为:![]() ;
;
[关联运用]过点F作直线l∥BA,交CA的延长线于点N,取AC的中点G,作C关于直线l的对称点M,连接MF、GF、MN

由对称性可得CF=MF,CN=MN,∠CNF=∠MNF
∵在等腰![]() 和等腰
和等腰![]() 中,
中,![]()
∴∠FED=∠BAC=45°,EF=DF=2,AC=BC=4
∴EF∥AC,CG=AG=![]() AC=2=EF
AC=2=EF
∴四边形CEFG为平行四边形
∴GF=CE
∴![]() =GF+MF≥MG(当且仅当G、F、M共线时,取等号)
=GF+MF≥MG(当且仅当G、F、M共线时,取等号)
∵直线l∥BA
∴四边形EFNA为平行四边形,∠CNF=∠BAC=45°
∴AN=EF=2,∠CNF=∠MNF=45°
∴GN=AG+AN=4,MN=CN=AC+AN=6,∠MNC=∠CNF+∠MNF=90°
根据勾股定理可得MG=![]()
∴![]() ≥
≥![]()
即![]() 的最小值为
的最小值为![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
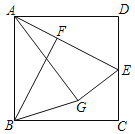
【题目】如图,在正方形ABCD中,E是CD边上一点,DE=2,过B作AE的垂线,垂足为点F,BF=3,将△ADE沿AE翻折,得到△AGE,AG与BF于点M,连接BG,则△BMG的周长为______
查看答案和解析>>
科目:初中数学 来源: 题型:
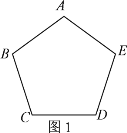
【题目】数学中我们学习了尺规作图,小明发现有些作图只用一种工具就可以完成,你能解决下列问题吗?
(1)请只用无刻度的直尺完成下列作图,不写画法,保留画图痕迹(用虚线表示画图过程,实线表示画图结果)在图1中,过点A画一条直线把正五边形ABCDE分成面积相等的两部分;
(2)已知直线l及l外一点A(按下列要求作图,不写画法,保留画图痕迹).
①在图2中,只用圆规在直线l上画出两点B、C,使得点A、B、C是一个等腰三角形的三个顶点;
②在图3中,只用圆规在直线l外画出一点P,使得点A、P所在直线与直线l平行.
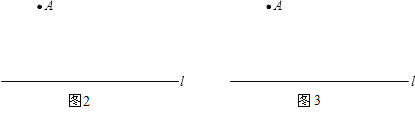
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
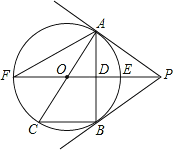
(1)求证:直线PA为⊙O的切线;
(2)试探究线段EF、OD、OP之间的等量关系,并加以证明;
(3)若BC=6,tan∠F=![]() ,求cos∠ACB的值和线段PE的长.
,求cos∠ACB的值和线段PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 在底边
在底边![]() 上,
上,![]() 的两边分别交
的两边分别交![]() 、
、![]() 所在直线于
所在直线于![]() 、
、![]() 两点,
两点,![]() ,
,![]() .
.
(1)如图1,若![]() ,
,![]() ,求证:
,求证:![]() ;
;
(2)如图2,求![]() 的值(含
的值(含![]() 的式子表示);
的式子表示);
(3)如图3,连接![]() ,若
,若![]() ,
,![]() ,且
,且![]() ,直接写出
,直接写出![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的顶点![]() ,经过点
,经过点![]() ,与
,与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
(1)求该抛物线的解析式;
(2)如图1,点![]() 是抛物线上的一个动点,且在直线
是抛物线上的一个动点,且在直线![]() 的下方,过点
的下方,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() ,当
,当![]() 取最大值时,求点
取最大值时,求点![]() 的坐标;
的坐标;
(3)如图2,![]() 轴交
轴交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() ,
,![]() 之间的一个动点,直线
之间的一个动点,直线![]() ,
,![]() 与
与![]() 分别交于
分别交于![]() ,
,![]() ,当点
,当点![]() 运动时.
运动时.
①直接写出![]() 的值;
的值;
②直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2019·信阳一模)如图,锐角三角形ABC中,BC=6,BC边上的高为4,直线MN交边AB于点M,交AC于点N,且MN∥BC,以MN为边作正方形MNPQ,设其边长为x(x>0),正方形MNPQ与△ABC公共部分的面积为y,则y与x的函数图象大致是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是CD边的中点,且BE⊥AC于点F,连接DF,则下列结论错误的是( )
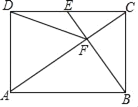
A.△ADC∽△CFBB.AD=DF
C.![]() =
=![]() D.
D.![]() =
=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com