
【题目】如图,在矩形ABCD中,E是CD边的中点,且BE⊥AC于点F,连接DF,则下列结论错误的是( )
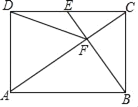
A.△ADC∽△CFBB.AD=DF
C.![]() =
=![]() D.
D.![]() =
=![]()
【答案】C
【解析】
依据∠ADC=∠BCD=90°,∠CAD=∠BCF,即可得到△ADC∽△CFB;过D作DM∥BE交AC于N,交AB于M,得出DM垂直平分AF,即可得到DF=DA;设CE=a,AD=b,则CD=2a,由△ADC∽△CFB,可得![]() ,可得b=
,可得b=![]() a,依据
a,依据![]() ,即可得出
,即可得出![]() ;根据E是CD边的中点,可得CE:AB=1:2,再根据△CEF∽△ABF,即可得到
;根据E是CD边的中点,可得CE:AB=1:2,再根据△CEF∽△ABF,即可得到![]() .
.
∵BE⊥AC,∠ADC=∠BCD=90°,
∴∠BCF+∠ACD=∠CAD+∠ACD,
∴∠CAD=∠BCF,
∴△ADC∽△CFB,故A选项正确;
如图,过D作DM∥BE交AC于N,交AB于M,
∵DE∥BM,BE∥DM,
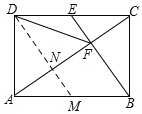
∴四边形BMDE是平行四边形,
∴BM=DE=![]() DC,
DC,
∴BM=AM,
∴AN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥AF,
∴DM垂直平分AF,
∴DF=DA,故B选项正确;
设CE=a,AD=b,则CD=2a,
∵∠ADC=∠BCD=90°,△ADC∽△CFB
∴∠CBE=∠DCA,
∴∠DAC=∠CEB,
∴△ADC∽△ECB,

由△ADC∽△ECB,可得![]() ,
,
即b=![]() a,
a,
∴![]() ,
,
AC=![]() ,
,
∴![]() ,故C选项错误;
,故C选项错误;
∵E是CD边的中点,
∴CE:AB=1:2,
又∵CE∥AB,
∴△CEF∽△ABF,
∴![]() ,故选D选项正确;
,故选D选项正确;
故选:C.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
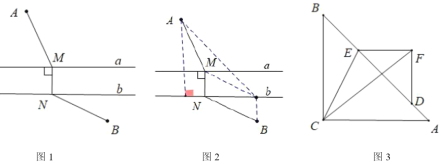
【题目】(问题探究)如图1,![]() ,直线
,直线![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 到直线
到直线![]() 的距离为2,点
的距离为2,点![]() 到
到![]() 的距离为1,
的距离为1,![]() ,
,![]() ,则
,则![]() 的最小值是______;(提示:将线段
的最小值是______;(提示:将线段![]() 沿
沿![]() 方向平移1个单位长度即可解决,如图2所示.)
方向平移1个单位长度即可解决,如图2所示.)
(关联运用)如图3,在等腰![]() 和等腰
和等腰![]() 中,
中,![]() ,
,![]() 在直线
在直线![]() 上,
上,![]() ,连接
,连接![]() 、
、![]() ,则
,则![]() 的最小值是______.
的最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水产养殖户进行小龙虾养殖. 已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,日销售量![]() 与时间第
与时间第![]() 天之间的函数关系式为
天之间的函数关系式为![]() (
(![]() ,
,![]() 为整数),销售单价
为整数),销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间满足一次函数关系如下表:
天之间满足一次函数关系如下表:
时间第 | 1 | 2 | 3 | … | 80 |
销售单价 | 49. 5 | 49 | 48. 5 | … | 10 |
(1)写出销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间的函数关系式;
天之间的函数关系式;
(2)在整个销售旺季的80天里,哪一天的日销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=2AB,对角线相交与O点,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列4个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④CF=BD.正确的结论是( )
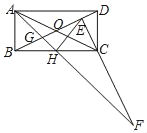
A.①②④B.①④C.③④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某风景区内一座塔AB的高度,小明分别在塔的对面一楼房CD的楼底C、楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度.(sin30°=0.50,cos30°≈0.87,tan30°≈0.58)
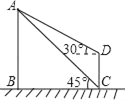
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”“一般”“较强”“很强”四个层次,并绘制成如下两幅尚不完整的统计图
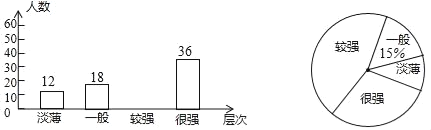
根据以上信息,解答下列问题:
(1)该校有1200名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,估计全校需要强化安全教育的学生约有多少名?
(2)请直接将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②![]() >0;③ac﹣b+1=0;④2a+b=0其中正确结论的个数是( )
>0;③ac﹣b+1=0;④2a+b=0其中正确结论的个数是( )
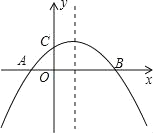
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com