
【题目】某水产养殖户进行小龙虾养殖. 已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,日销售量![]() 与时间第
与时间第![]() 天之间的函数关系式为
天之间的函数关系式为![]() (
(![]() ,
,![]() 为整数),销售单价
为整数),销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间满足一次函数关系如下表:
天之间满足一次函数关系如下表:
时间第 | 1 | 2 | 3 | … | 80 |
销售单价 | 49. 5 | 49 | 48. 5 | … | 10 |
(1)写出销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间的函数关系式;
天之间的函数关系式;
(2)在整个销售旺季的80天里,哪一天的日销售利润最大?最大利润是多少?
【答案】(1)![]() ;(2)第19天的日销售利润最大,最大利润是4761元.
;(2)第19天的日销售利润最大,最大利润是4761元.
【解析】
(1)设销售单价p(元/kg)与时间第t天之间的函数关系式为:p=kt+b,将(1,49.5),(2,49)代入,再解方程组即可得到结论;
(2)设每天获得的利润为w元,由题意根据利润=销售额-成本,可得到w=-(t-19)2+4761,根据二次函数的性质即可得到结论.
(1)设销售单价![]() (元
(元![]() )与时间第
)与时间第![]() 天之间的函数关系式为:
天之间的函数关系式为:![]() ,
,
将![]() 代入,得
代入,得![]() ,
,
解得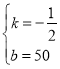 .
.
∴销售单价![]() (元
(元![]() )与时间第
)与时间第![]() 天之间的函数关系式为
天之间的函数关系式为![]() .
.
(2)设每天获得的利润为![]() 元.
元.
由题意,得![]()
![]()
![]() .
.
∵![]() ,
,
∴![]() 有最大值. 当
有最大值. 当![]() 时,
时, ![]() 最大,此时,
最大,此时,![]() (元)
(元)
答:第19天的日销售利润最大,最大利润是4761元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】数学中我们学习了尺规作图,小明发现有些作图只用一种工具就可以完成,你能解决下列问题吗?
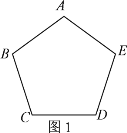
(1)请只用无刻度的直尺完成下列作图,不写画法,保留画图痕迹(用虚线表示画图过程,实线表示画图结果)在图1中,过点A画一条直线把正五边形ABCDE分成面积相等的两部分;
(2)已知直线l及l外一点A(按下列要求作图,不写画法,保留画图痕迹).
①在图2中,只用圆规在直线l上画出两点B、C,使得点A、B、C是一个等腰三角形的三个顶点;
②在图3中,只用圆规在直线l外画出一点P,使得点A、P所在直线与直线l平行.
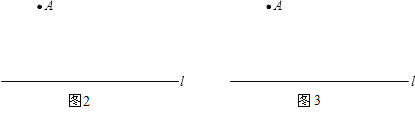
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的顶点![]() ,经过点
,经过点![]() ,与
,与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
(1)求该抛物线的解析式;
(2)如图1,点![]() 是抛物线上的一个动点,且在直线
是抛物线上的一个动点,且在直线![]() 的下方,过点
的下方,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() ,当
,当![]() 取最大值时,求点
取最大值时,求点![]() 的坐标;
的坐标;
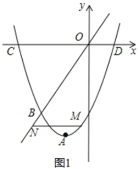
(3)如图2,![]() 轴交
轴交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() ,
,![]() 之间的一个动点,直线
之间的一个动点,直线![]() ,
,![]() 与
与![]() 分别交于
分别交于![]() ,
,![]() ,当点
,当点![]() 运动时.
运动时.
①直接写出![]() 的值;
的值;
②直接写出![]() 的值.
的值.
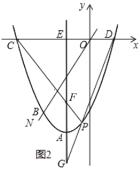
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2019·信阳一模)如图,锐角三角形ABC中,BC=6,BC边上的高为4,直线MN交边AB于点M,交AC于点N,且MN∥BC,以MN为边作正方形MNPQ,设其边长为x(x>0),正方形MNPQ与△ABC公共部分的面积为y,则y与x的函数图象大致是( )

A.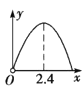 B.
B. C.
C.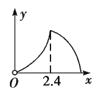 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察猜想,如图①点B、A、C在同一条直线上,DB⊥BC,EC⊥BC且∠DAE=90°,AD=AE,则BC、BD、CE之间的数量关系为 ;
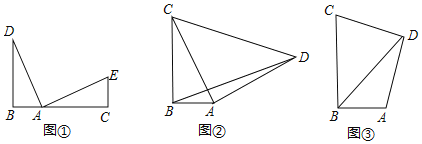
(2)问题解决,如图②,在Rt△ABC中,∠ABC=90°,CB=6,AB=3,以AC为直角边向外作等腰Rt△DAC,连结BD,求BD的长;
(3)拓展延伸,如图③,在四边形ABCD中,∠ABC=∠ADC=90°,CB=6,AB=3,DC=DA,请直接写出BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=45°,将△ABC绕点A逆时针方向旋转得△AEF,其中,E,F是点B,C旋转后的对应点,BE,CF相交于点D.若四边形ABDF为菱形,则∠CAE的大小是( )
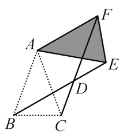
A.90°B.75°C.60°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A,B两城决定向C,D两乡运送肥料以支持农村生产.已知A,B两城共有肥料500吨,其中A城肥料比B城肥料少100吨,从A,B城往C,D两乡运肥料的平均费用如表:
A城 | B城 | |
C乡 | 20元/吨 | 15元/吨 |
D乡 | 25元/吨 | 30元/吨 |
现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从B城运往D乡x吨肥料,总运费为y元,求y与x之间的函数关系,并说明如何安排运输才能使得总运费最小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是CD边的中点,且BE⊥AC于点F,连接DF,则下列结论错误的是( )
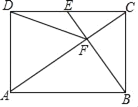
A.△ADC∽△CFBB.AD=DF
C.![]() =
=![]() D.
D.![]() =
=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
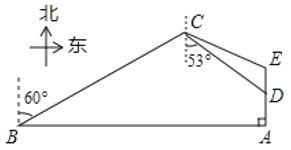
【题目】如图,我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪,船长马上向我国渔政搜救中心发出求救信号,此时一艘渔政船正巡航到捕鱼船正西方向的B处,该渔政船收到渔政求救中心指令后前去救援,但两船之间有大片暗礁,无法直线到达,于是决定马上调整方向,先向北偏东60°方向以每小时40海里的速度航行半小时到达C处,同时捕鱼船低速航行到A点的正北2海里D处,渔政船航行到点C处时测得点D在南偏东53°方向上.
(1)求CD两点的距离;
(2)渔政船决定再次调整航向前去救援,若两船航速不变,并且在点E处相会合,求∠ECD的正弦值.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com