
【题目】(1)观察猜想,如图①点B、A、C在同一条直线上,DB⊥BC,EC⊥BC且∠DAE=90°,AD=AE,则BC、BD、CE之间的数量关系为 ;
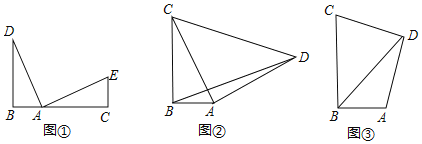
(2)问题解决,如图②,在Rt△ABC中,∠ABC=90°,CB=6,AB=3,以AC为直角边向外作等腰Rt△DAC,连结BD,求BD的长;
(3)拓展延伸,如图③,在四边形ABCD中,∠ABC=∠ADC=90°,CB=6,AB=3,DC=DA,请直接写出BD的长.
【答案】(1)BC=BD+CE;(2)3![]() ;(3)
;(3)![]() .
.
【解析】
(1)观察猜想:证明![]() ,可得结论:
,可得结论:![]() ;
;
(2)问题解决:作辅助线,同理证明:![]() ,可得
,可得![]() ,
,![]() ,最后利用勾股定理求
,最后利用勾股定理求![]() 的长;
的长;
(3)拓展延伸:同理证明三角形全等,设![]() ,
,![]() ,根据全等三角形对应边相等列方程组可得结论.
,根据全等三角形对应边相等列方程组可得结论.
解:(1)观察猜想
结论:BC=BD+CE,理由是:
如图①,∵∠B=90°,∠DAE=90°,
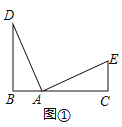
∴∠D+∠DAB=∠DAB+∠EAC=90°,
∴∠D=∠EAC,
∵∠B=∠C=90°,AD=AE,
∴△ADB≌△EAC(AAS),
∴BD=AC,EC=AB,
∴BC=AB+AC=BD+CE;
故答案为:BC=BD+CE;
(2)问题解决
如图②,过D作DE⊥AB,交BA的延长线于E,
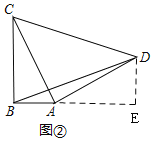
由(1)同理得:△ABC≌△DEA,
∴DE=AB=3,AE=BC=6,
Rt△BDE中,BE=9,
由勾股定理得:![]() ;
;
(3)拓展延伸
如图③,过D作DE⊥BC于E,作DF⊥AB于F,
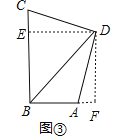
同理得:△CED≌△AFD,
∴CE=AF,ED=DF,
设AF=x,DF=y,
则![]() ,解得:
,解得:![]() ,
,
![]() ,
,![]() ,
,
由勾股定理得:![]() .
.


科目:初中数学 来源: 题型:
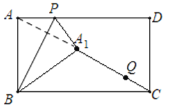
【题目】如图,在矩形ABCD中,![]() ,AD=9,点P是AD边上的一个动点,连接BP,将矩形ABCD沿BP折叠,得到△A1PB,连接A1C,取A1C的三等分点Q(CQ<A1Q),当点P从点A出发,沿边AD运动到点D时停止运动,点Q的运动路径长为( )
,AD=9,点P是AD边上的一个动点,连接BP,将矩形ABCD沿BP折叠,得到△A1PB,连接A1C,取A1C的三等分点Q(CQ<A1Q),当点P从点A出发,沿边AD运动到点D时停止运动,点Q的运动路径长为( )
A.πB.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明投掷一次骰子,向上一面的点数记为![]() ,再投掷一次骰子,向上一面的点数记为
,再投掷一次骰子,向上一面的点数记为![]() ,这样就确定点
,这样就确定点![]() 的一个坐标
的一个坐标![]() ,那么点
,那么点![]() 落在双曲线
落在双曲线![]() 上的概率为( )
上的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
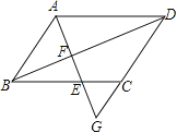
【题目】如图,在平行四边形ABCD中,点G在边DC的延长线上,AG交边BC于点E,交对角线BD于点F.
(1)求证:AF2=EFFG;
(2)如果EF=![]() ,FG=
,FG=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校八年级共400名学生,为了解该年级学生的视力情况,从中随机抽取40名学生的视力数据作为样本,数据统计如下:
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
根据数据绘制了如下的表格和统计图:
等级 | 视力(x) | 频数 | 频率 |
|
| 4 | 0.1 |
|
| 12 | 0.3 |
|
|
| |
|
|
| |
| 10 | 0.25 | |
合计 | 40 | 1 | |
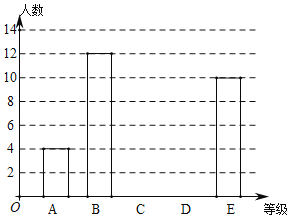
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该校八年级学生视力为“![]() 级”的有多少人?
级”的有多少人?
(4)该年级学生会宣传部有2名男生和2名女生,现从中随机挑选2名同学参加“防控近视,爱眼护眼”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水产养殖户进行小龙虾养殖. 已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,日销售量![]() 与时间第
与时间第![]() 天之间的函数关系式为
天之间的函数关系式为![]() (
(![]() ,
,![]() 为整数),销售单价
为整数),销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间满足一次函数关系如下表:
天之间满足一次函数关系如下表:
时间第 | 1 | 2 | 3 | … | 80 |
销售单价 | 49. 5 | 49 | 48. 5 | … | 10 |
(1)写出销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间的函数关系式;
天之间的函数关系式;
(2)在整个销售旺季的80天里,哪一天的日销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△DEF均为等腰直角三角形,AB=2,DE=1,E、B、F、C在同一条直线上,开始时点B与点F重合,让△DEF沿直线BC向右移动,最后点C与点E重合,设两三角形重合面积为y,点F移动的距离为x,则y关于x的大致图象是( )

A.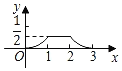 B.
B.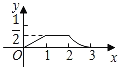
C.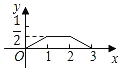 D.
D.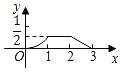
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某风景区内一座塔AB的高度,小明分别在塔的对面一楼房CD的楼底C、楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度.(sin30°=0.50,cos30°≈0.87,tan30°≈0.58)
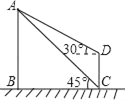
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个三角板ABC,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2).

(1)当点C落在边EF上时,x= cm;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)设边BC的中点为点M,边DF的中点为点N.直接写出在三角板平移过程中,点M与点N之间距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com