
����Ŀ���������ǰ�ABC��DEF������ͼ��ʾ��λ�ðڷţ���B���D�غϣ���AB���DE��ͬһ��ֱ���ϣ�����ͼ�������еĵ㣬�߶���ͬһƽ���ڣ������У���C=��DEF=90������ABC=��F=30����AC=DE=6cm���̶ֹ����ǰ�DEF�������ǰ�ABC������DE����ƽ�ƣ�����C���ڱ�EF��ʱֹͣ�˶��������ǰ�ƽ�Ƶľ���Ϊx��cm�����������ǰ��ص����ֵ����Ϊy��cm2����

��1������C���ڱ�EF��ʱ��x= cm��
��2����y����x�ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
��3�����BC���е�Ϊ��M����DF���е�Ϊ��N��ֱ��д�������ǰ�ƽ�ƹ����У���M���N֮��������Сֵ��
���𰸡���1��15����2��![]()
![]()
![]() ����3��
����3��![]() ��
��
��������
��1����������Ǻ������õ�BG�ij��������ɵ�GE�ij����ɾ��ε����ʣ��ɵô𰸣�
��2���������ۣ�����0��t��6ʱ�����������ε������ʽ���ɵô𰸣�����6��t��12ʱ������12��t��15ʱ����������ĺͲ�ɵô𰸣�
��3�����ݵ���ֱ�������е�������д��߶���̣��ɵ�M���߶�NG�ϣ����������ε���λ�ߣ��ɵ�NG�ij�������������Ǻ������ɵ�MG�ij��������߶εĺͲ�ɵô𰸣�
�⣺��1����ͼ1��ʾ����CG��AB��G�㣮
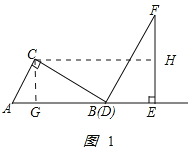 ��
��
��Rt��ABC�У���AC=6����ABC=30���ã�BC=![]() =
=![]() ����Rt��BCG�У�BG=BCcos30��=9���ı���CGEH�Ǿ��Σ�CH=GE=BG+BE=9+6=15cm���ʴ�Ϊ15��
����Rt��BCG�У�BG=BCcos30��=9���ı���CGEH�Ǿ��Σ�CH=GE=BG+BE=9+6=15cm���ʴ�Ϊ15��
��2������0��x��6ʱ����ͼ2��ʾ��
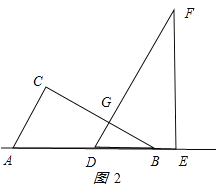 ��
��
��GDB=60������GBD=30����DB=x���ã�DG=![]() ��BG=
��BG=![]() ���ص����ֵ����Ϊy=
���ص����ֵ����Ϊy=![]() DGBG=
DGBG=![]() ��
��![]() ��
��![]() =
=![]() ��
��
����6��x��12ʱ����ͼ3��ʾ��
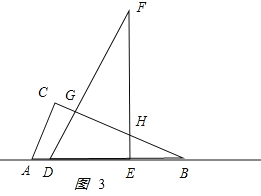 ��
��
BD=x��DG=![]() ��BG=
��BG=![]() ��BE=x��6��EH=
��BE=x��6��EH=![]() ���ص����ֵ����Ϊy=
���ص����ֵ����Ϊy=![]() =
=![]() DGBG��
DGBG��![]() BEEH����y=
BEEH����y=![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() ��
��
����12��x��15ʱ����ͼ4��ʾ��
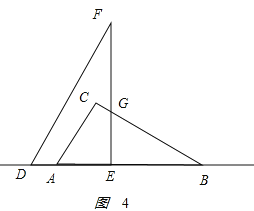 ��
��
AC=6��BC=![]() ��BD=x��BE=��x��6����EG=
��BD=x��BE=��x��6����EG=![]() ���ص����ֵ����Ϊy=
���ص����ֵ����Ϊy=![]() =
=![]() ACBC��
ACBC��![]() BEEG����y=
BEEG����y=![]() ������
������![]() =
=![]() ��
��
����������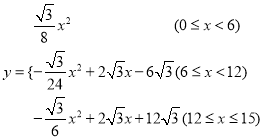 ��
��
��3����ͼ5��ʾ��NG��DE��G�㣮
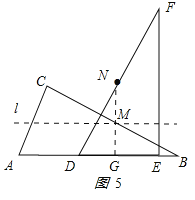 ��
��
��M��NG��ʱMN��̣�NG����DEF����λ�ߣ�NG=![]() EF=
EF=![]() ��
��
MB=![]() CB=
CB=![]() ����B=30����MG=
����B=30����MG=![]() MB=
MB=![]() ��
��
MN��С=![]() =
=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���۲���룬��ͼ�ٵ�B��A��C��ͬһ��ֱ���ϣ�DB��BC��EC��BC�ҡ�DAE��90����AD��AE����BC��BD��CE֮���������ϵΪ�� ����
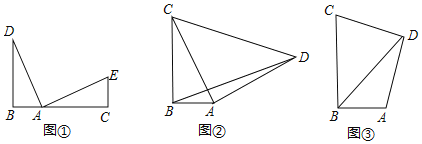
��2������������ͼ�ڣ���Rt��ABC�У���ABC��90����CB��6��AB��3����ACΪֱ�DZ�����������Rt��DAC������BD����BD�ij���
��3����չ���죬��ͼ�ۣ����ı���ABCD�У���ABC����ADC��90����CB��6��AB��3��DC��DA����ֱ��д��BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
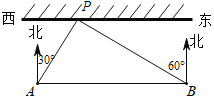
����Ŀ��Ϊ�˱�֤���������������к���ˮ��˳���ٰ죬ij���Ź�����Ա�˿�ͧ������ˮ��ˮ�飬��ÿ��10���ٶ���ƽ���ڰ��ߵ�����AB��������ʻ����A����ð���һ������P�ڱ�ƫ��30�������ϣ�������ʻ40�뵽��B��ʱ����ý�����P�ڱ�ƫ��60�������ϣ���ͼ��ʾ��������P������AB�ľ��루����������ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ϣ������Ѹ�ͷ�չ������ȥ�̳������֧����ʽ���Ӷ�������ݣ�ijУ��ѧ��ȤС�������һ�ݵ����ʾ���Ҫ��ÿ��ѡ��ֻѡһ������ϲ����֧����ʽ���ֽ�����������ͳ�Ʋ����Ƴ�����������������ͳ��ͼ������ͼ����������Ϣ����������⣺
��1����λ���������� ���ˣ�������ͳ��ͼ�У���ʾ��֧������֧��������Բ�ĽǵĶ���Ϊ�� ����
��2��������ͳ��ͼ�����������۲��ͼ��֧����ʽ���������������� ������
��3����һ�ι����У�С����С�����������������֧�������������п�������֧����ʽ��ѡһ�ַ�ʽ����֧�������û���״ͼ���б���ķ������������ǡ��ѡ��ͬһ��֧����ʽ�ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ��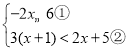 ����������գ���ɱ���Ľ��
����������գ���ɱ���Ľ��
�������ⲻ��ʽ�������� ����
�������ⲻ��ʽ�������� ����
�������Ѳ���ʽ�������Ľ��������ϱ�ʾ������
������ԭ����ʽ��Ľ⼯Ϊ�� ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
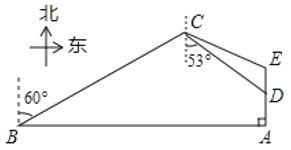
����Ŀ����ͼ�����Ϻ�ij����A����һ�Ҳ��㴬����ҵʱͻ���ش���ˣ������������ҹ������Ѿ����ķ�������źţ���ʱһ����������Ѳ�������㴬���������B�������������յ������������ָ���ǰȥ��Ԯ��������֮���д�Ƭ��������ֱ�ߵ�����Ǿ������ϵ�����������ƫ��60��������ÿСʱ40������ٶȺ��а�Сʱ����C����ͬʱ���㴬���ٺ��е�A�������2����D�������������е���C��ʱ��õ�D����ƫ��53�������ϣ�
��1����CD����ľ��룻
��2�������������ٴε�������ǰȥ��Ԯ�����������ٲ��䣬�����ڵ�E�����ϣ����ECD������ֵ�����ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
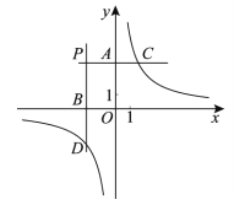
����Ŀ����ͼ���ֱ���ڶ������ڵĵ�![]() ��
��![]() ��
��![]() ���ƽ���ߣ���
���ƽ���ߣ���![]() ��
��![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ��
��![]() ����˫����
����˫����![]() �ֱ��ڵ�
�ֱ��ڵ�![]() ��
��![]() ��
��
�����������ۣ�
�ٴ�����������![]() ʹ
ʹ![]() ��
��
�ڴ�����������![]() ʹ
ʹ![]() ��
��
�۴�����������![]() ʹ
ʹ![]() ��
��
������ȷ���۵������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
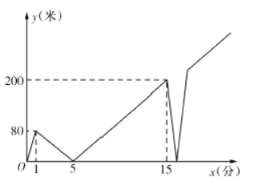
����Ŀ��һ���峿���ס���������һ����ֱ�ĵ�·��ͬ��㡢ͬ�յ������ܲ���������![]() ���Ӻ����ٳ����������ϼ�ʱ���ӿ��ٶ���ǰ�ܣ��ȵ����յ�������Լӿ����ٶȷ�����㣮��֪����ǰ����ֱ𱣳������ܣ���ȫ�̾�������������ͼ�Ǽ�������֮��ľ���
���Ӻ����ٳ����������ϼ�ʱ���ӿ��ٶ���ǰ�ܣ��ȵ����յ�������Լӿ����ٶȷ�����㣮��֪����ǰ����ֱ𱣳������ܣ���ȫ�̾�������������ͼ�Ǽ�������֮��ľ���![]() ���ף�����ܲ���ʱ��
���ף�����ܲ���ʱ��![]() ���֣��IJ��ֺ���ͼ�����ҵ�һ�ε����յ�ʱ�������______�ף�
���֣��IJ��ֺ���ͼ�����ҵ�һ�ε����յ�ʱ�������______�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=![]() x2+bx+c������ABC���������㣬���е�A��0��1������B����9��10����AC��x�ᣬ��Pʱֱ��AC�·��������ϵĶ��㣮
x2+bx+c������ABC���������㣬���е�A��0��1������B����9��10����AC��x�ᣬ��Pʱֱ��AC�·��������ϵĶ��㣮

��1���������ߵĽ���ʽ����2������P����y��ƽ�е�ֱ��l��ֱ��AB��AC�ֱ��ڵ�E��F�����ı���AECP��������ʱ�����P�����ꣻ
��3������PΪ�����ߵĶ���ʱ����ֱ��AC���Ƿ���ڵ�Q��ʹ����C��P��QΪ��������������ABC���ƣ������ڣ������Q�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com