
【题目】已知数轴上点![]() 与点
与点![]() 之间的距的距离为
之间的距的距离为![]() 个单位长度,点
个单位长度,点![]() 在原点的左侧,到原点的距离为
在原点的左侧,到原点的距离为![]() 个单位长度,点
个单位长度,点![]() 在点
在点![]() 的右侧,点
的右侧,点![]() 表示的数与点
表示的数与点![]() 表示的数互为相反数,动点
表示的数互为相反数,动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 移动,设移动时间为
移动,设移动时间为![]() 秒.
秒.
(1)点![]() 表示的数为 ,点
表示的数为 ,点![]() 表示的数为 ,点
表示的数为 ,点![]() 表示的数为 .
表示的数为 .
(2)用含![]() 的代数式分别表示点
的代数式分别表示点![]() 到点
到点![]() 和点
和点![]() 的距离:
的距离:![]() ,
,![]() .
.
(3)当点![]() 运动到
运动到![]() 点时,点
点时,点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度向
个单位长度的速度向![]() 点运动,点
点运动,点![]() 到达
到达![]() 点后,立即以同样的速度返回点
点后,立即以同样的速度返回点![]() ,在点
,在点![]() 开始运动后,当
开始运动后,当![]() 两点之间的距离为
两点之间的距离为![]() 个单位长度时,求此时点
个单位长度时,求此时点![]() 表示的数.
表示的数.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)根据点![]() 在原点的左侧,到原点的距离为
在原点的左侧,到原点的距离为![]() 个单位长度,可得知A表示的数为
个单位长度,可得知A表示的数为![]() ,然后结合数轴的性质以及相反数的性质进一步求解即可;
,然后结合数轴的性质以及相反数的性质进一步求解即可;
(2)根据题意可得PA相当于P点的运动距离,而PC可由ABPA计算即可;
(3)根据题意,分Q点到C点之前与到达C点返回两种情况进一步讨论即可.
(1)∵点![]() 在原点的左侧,到原点的距离为
在原点的左侧,到原点的距离为![]() 个单位长度,
个单位长度,
∴点A表示的数为![]() ,
,
∵点![]() 与点
与点![]() 之间的距的距离为
之间的距的距离为![]() 个单位长度,点
个单位长度,点![]() 在点
在点![]() 的右侧,
的右侧,
∴点![]() 表示的数为
表示的数为![]() ,
,
∵点![]() 表示的数与点
表示的数与点![]() 表示的数互为相反数,
表示的数互为相反数,
∴点![]() 表示的数为12,
表示的数为12,
故答案为:![]() ,
,![]() ,
,![]() ;
;
(2)由题意可得:PA相当于P点的运动距离,
∴PA=![]() ,
,
∴PC=ABPA=![]() ,
,
故答案为:![]() ,
,![]() ;
;
(3)设![]() 、
、![]() 两点之间的距离为
两点之间的距离为![]() 时,点
时,点![]() 的运动时间为
的运动时间为![]() 秒,
秒,
此时点![]() 表示的数是
表示的数是![]() .
.
当![]() 时,
时,![]() 秒时点
秒时点![]() 表示的数是
表示的数是![]() ,
,
则![]()
![]() ,或
,或![]()
![]()
![]() ,
,
解得m=7或5,
∴此时点![]() 表示的数是
表示的数是![]() 或
或![]() ;
;
当![]() 时,
时,![]() 秒后点
秒后点![]() 表示的数是
表示的数是![]() ,
,
则![]()
![]() ,或
,或![]()
![]()
![]() =2,
=2,
解得![]() 或
或![]() ,
,
∴此时点![]() 表示的数是
表示的数是![]() 或
或![]() .
.
综上,当![]() 、
、![]() 两点之间的距离为
两点之间的距离为![]() 时,此时点
时,此时点![]() 表示的数可以是
表示的数可以是![]() ,
,![]() ,
,![]() ,
,![]() .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:
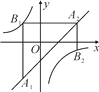
【题目】如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-![]() 上,并且满足A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2018=_______.
上,并且满足A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2018=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公共汽车行驶在笔直的公路上,这条路上有![]() 四个站点,每相邻两站之间的距离为
四个站点,每相邻两站之间的距离为![]() 千米,从
千米,从![]() 站开往
站开往![]() 站的车称为上行车,从
站的车称为上行车,从![]() 站开往
站开往![]() 站的车称为下行车.第一班上行车、下行车分别从
站的车称为下行车.第一班上行车、下行车分别从![]() 站、
站、![]() 站同时发车,相向而行,且以后上行车、下行车每隔
站同时发车,相向而行,且以后上行车、下行车每隔![]() 分钟分别在
分钟分别在![]() 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、 下行车的速度均为
站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、 下行车的速度均为![]() 千米/小时.
千米/小时.
![]() 第一班上行车到
第一班上行车到![]() 站、第一班下行车到
站、第一班下行车到![]() 站分别用时多少?
站分别用时多少?
![]() 第一班上行车与第一班下行车发车后多少小时相距
第一班上行车与第一班下行车发车后多少小时相距![]() 千米?
千米?
![]() 一乘客在
一乘客在![]() 两站之间的
两站之间的![]() 处,刚好遇到上行车,
处,刚好遇到上行车,![]() 千米,他从
千米,他从![]() 处以
处以![]() 千米/小时的速度步行到
千米/小时的速度步行到![]() 站乘下行车前往
站乘下行车前往![]() 站办事.
站办事.

①若![]() 千米,乘客从
千米,乘客从![]() 处到达
处到达![]() 站的时间最少要几分钟?
站的时间最少要几分钟?
②若![]() 千米,乘客从
千米,乘客从![]() 处到达
处到达![]() 站的时间最少要几分钟?
站的时间最少要几分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如 图,△ACB和△E CD都是等腰直角三角形,A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于F.
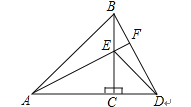
(1)求证:△ACE≌△BCD;
(2)直线AE与BD互相垂直吗?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.
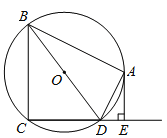
(1)求证:AE是⊙O的切线;
(2)如果AB=4,AE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角系xOy中,直线AB交x轴正半轴于点A,交y轴负半轴于点B,B点的坐标为B(0,﹣6),点C在线段OA上,将△ABC沿直线BC翻折,点A与y轴上的点D(0,4),恰好重合.
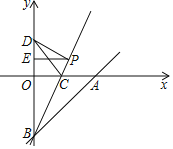
(1)求A点、C点的坐标;
(2)在y轴是否存在一点H,使得△HAB和△ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由
(3)已知点E(0,3),P是直线BC上一动点(P不与B重合),连接PD、PE,求△PDE周长的最小值,并求出此BP长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了开展“阳光体育运动”,计划购买篮球与足球共![]() 个,已知每个篮球的价格为
个,已知每个篮球的价格为![]() 元,每个足球的价格为
元,每个足球的价格为![]() 元
元
(1)若购买这两类球的总金额为![]() 元,求篮球和足球各购买了多少个?
元,求篮球和足球各购买了多少个?
(2)元旦期间,商家给出蓝球打九折,足球打八五折的优惠价,若购买这种篮球与足球各![]() 个,那么购买这两类球一共需要多少钱?
个,那么购买这两类球一共需要多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形![]() 中,点
中,点![]() 是
是![]() 上一点,过点
上一点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,连结
,连结![]() .
.
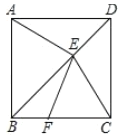
(1)已知点![]() 在线段
在线段![]() 上.
上.
①若![]() ,求
,求![]() 度数;
度数;
②求证:![]() .
.
(2)已知正方形边长为![]() ,且
,且![]() ,请直接写出线段
,请直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平行四边形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,
的中点,![]() 过点
过点![]() 与
与![]() ,
,![]() 分别相交于
分别相交于![]() ,
,![]() ,
,![]() 过点
过点![]() 与
与![]() ,
,![]() 分别相交于点
分别相交于点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,若![]() ,
,![]() ,在不添加任何辅助的情况下,请直接写出图2中与四边形
,在不添加任何辅助的情况下,请直接写出图2中与四边形![]() 面积相等的所有的平行四边形(四边形
面积相等的所有的平行四边形(四边形![]() 除外).
除外).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com