
ЁОЬтФПЁПШчЭМЃЌЙЋЙВЦћГЕааЪЛдкБЪжБЕФЙЋТЗЩЯЃЌетЬѕТЗЩЯга![]() ЫФИіеОЕуЃЌУПЯрСкСНеОжЎМфЕФОрРыЮЊ
ЫФИіеОЕуЃЌУПЯрСкСНеОжЎМфЕФОрРыЮЊ![]() ЧЇУзЃЌДг
ЧЇУзЃЌДг![]() еОПЊЭљ
еОПЊЭљ![]() еОЕФГЕГЦЮЊЩЯааГЕЃЌДг
еОЕФГЕГЦЮЊЩЯааГЕЃЌДг![]() еОПЊЭљ
еОПЊЭљ![]() еОЕФГЕГЦЮЊЯТааГЕЃЎЕквЛАрЩЯааГЕЁЂЯТааГЕЗжБ№Дг
еОЕФГЕГЦЮЊЯТааГЕЃЎЕквЛАрЩЯааГЕЁЂЯТааГЕЗжБ№Дг![]() еОЁЂ
еОЁЂ![]() еОЭЌЪБЗЂГЕЃЌЯрЯђЖјааЃЌЧввдКѓЩЯааГЕЁЂЯТааГЕУПИє
еОЭЌЪБЗЂГЕЃЌЯрЯђЖјааЃЌЧввдКѓЩЯааГЕЁЂЯТааГЕУПИє![]() ЗжжгЗжБ№дк
ЗжжгЗжБ№дк![]() еОЭЌЪБЗЂвЛАрГЕЃЌГЫПЭжЛФмЕНеОЕуЩЯЁЂЯТГЕ(ЩЯЁЂЯТГЕЕФЪБМфКіТдВЛМЦ)ЃЌЩЯааГЕЁЂ ЯТааГЕЕФЫйЖШОљЮЊ
еОЭЌЪБЗЂвЛАрГЕЃЌГЫПЭжЛФмЕНеОЕуЩЯЁЂЯТГЕ(ЩЯЁЂЯТГЕЕФЪБМфКіТдВЛМЦ)ЃЌЩЯааГЕЁЂ ЯТааГЕЕФЫйЖШОљЮЊ![]() ЧЇУз/аЁЪБЃЎ
ЧЇУз/аЁЪБЃЎ
![]() ЕквЛАрЩЯааГЕЕН
ЕквЛАрЩЯааГЕЕН![]() еОЁЂЕквЛАрЯТааГЕЕН
еОЁЂЕквЛАрЯТааГЕЕН![]() еОЗжБ№гУЪБЖрЩйЃП
еОЗжБ№гУЪБЖрЩйЃП
![]() ЕквЛАрЩЯааГЕгыЕквЛАрЯТааГЕЗЂГЕКѓЖрЩйаЁЪБЯрОр
ЕквЛАрЩЯааГЕгыЕквЛАрЯТааГЕЗЂГЕКѓЖрЩйаЁЪБЯрОр![]() ЧЇУзЃП
ЧЇУзЃП
![]() вЛГЫПЭдк
вЛГЫПЭдк![]() СНеОжЎМфЕФ
СНеОжЎМфЕФ![]() ДІЃЌИеКУгіЕНЩЯааГЕЃЌ
ДІЃЌИеКУгіЕНЩЯааГЕЃЌ![]() ЧЇУзЃЌЫћДг
ЧЇУзЃЌЫћДг![]() ДІвд
ДІвд![]() ЧЇУз/аЁЪБЕФЫйЖШВНааЕН
ЧЇУз/аЁЪБЕФЫйЖШВНааЕН![]() еОГЫЯТааГЕЧАЭљ
еОГЫЯТааГЕЧАЭљ![]() еОАьЪТЃЎ
еОАьЪТЃЎ

ЂйШє![]() ЧЇУзЃЌГЫПЭДг
ЧЇУзЃЌГЫПЭДг![]() ДІЕНДя
ДІЕНДя![]() еОЕФЪБМфзюЩйвЊМИЗжжгЃП
еОЕФЪБМфзюЩйвЊМИЗжжгЃП
ЂкШє![]() ЧЇУзЃЌГЫПЭДг
ЧЇУзЃЌГЫПЭДг![]() ДІЕНДя
ДІЕНДя![]() еОЕФЪБМфзюЩйвЊМИЗжжгЃП
еОЕФЪБМфзюЩйвЊМИЗжжгЃП
ЁОД№АИЁПЃЈ1ЃЉЕквЛАрЩЯааГЕЕН![]() еОгУЪБ
еОгУЪБ![]() аЁЪБЃЌЕквЛАрЯТааГЕЕН
аЁЪБЃЌЕквЛАрЯТааГЕЕН![]() еОгУЪБ
еОгУЪБ![]() аЁЪБЃЛЃЈ2ЃЉЕквЛАрЩЯааГЕгыЕквЛАрЯТааГЕЗЂГЕКѓ
аЁЪБЃЛЃЈ2ЃЉЕквЛАрЩЯааГЕгыЕквЛАрЯТааГЕЗЂГЕКѓ![]() аЁЪБЛђ
аЁЪБЛђ![]() аЁЪБЯрОр
аЁЪБЯрОр![]() ЧЇУзЃЛЃЈ3ЃЉЂй
ЧЇУзЃЛЃЈ3ЃЉЂй![]() ЧЇУзЃЌГЫПЭДг
ЧЇУзЃЌГЫПЭДг![]() ДІЕНДя
ДІЕНДя![]() еОЕФЪБМфзюЩйвЊ
еОЕФЪБМфзюЩйвЊ![]() ЗжжгЃЛЂк
ЗжжгЃЛЂк![]() ЧЇУзЃЌГЫПЭДг
ЧЇУзЃЌГЫПЭДг![]() ДІЕНДя
ДІЕНДя![]() еОЕФЪБМфзюЩйвЊ
еОЕФЪБМфзюЩйвЊ![]() ЗжжгЃЎ
ЗжжгЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЪБМф=ТЗГЬЁТЫйЖШМЦЫуМДПЩЃЛ
ЃЈ2ЃЉЩшЕквЛАрЩЯааГЕгыЕквЛАрЯТааГЕЗЂГЕtаЁЪБЯрОр![]() ЧЇУзЃЌШЛКѓИљОнЯргіЧАКЭЯргіКѓЗжРрЬжТлЃЌЗжБ№СаГіЖдгІИіЗНГЬМДПЩЧѓГіtЃЛ
ЧЇУзЃЌШЛКѓИљОнЯргіЧАКЭЯргіКѓЗжРрЬжТлЃЌЗжБ№СаГіЖдгІИіЗНГЬМДПЩЧѓГіtЃЛ
ЃЈ3ЃЉгЩЬтвтжЊЃКЭЌЪБГіЗЂЕФвЛЖдЩЯЁЂЯТааГЕЕФЮЛжУЙигк![]() жаЕуЖдГЦЃЌГЫПЭгвВрЕквЛСОЯТааГЕРы
жаЕуЖдГЦЃЌГЫПЭгвВрЕквЛСОЯТааГЕРы![]() еОвВЪЧ
еОвВЪЧ![]() ЧЇУзЃЌетСОЯТааГЕРы
ЧЇУзЃЌетСОЯТааГЕРы![]() еОЪЧ
еОЪЧ![]() ЧЇУз
ЧЇУз
ЂйЯШЧѓГіЕуPЕНЕуBЕФЪБМфКЭГЫПЭгвВрЕквЛСОЯТааГЕЕНДя![]() еОЕФЪБМфЃЌБШНЯМДПЩХаЖЯГЫПЭФмЗёГЫЩЯгвВрЕквЛСОЯТааГЕЃЌДгЖјЧѓГіГЫПЭДг
еОЕФЪБМфЃЌБШНЯМДПЩХаЖЯГЫПЭФмЗёГЫЩЯгвВрЕквЛСОЯТааГЕЃЌДгЖјЧѓГіГЫПЭДг![]() ДІЕНДя
ДІЕНДя![]() еОЕФзюЩйЪБМфЃЛ
еОЕФзюЩйЪБМфЃЛ
ЂкЯШЧѓГіЕуPЕНЕуBЕФЪБМфКЭГЫПЭгвВрЕквЛСОЯТааГЕЕНДя![]() еОЕФЪБМфЃЌБШНЯМДПЩХаЖЯГЫПЭФмЗёГЫЩЯгвВрЕквЛСОЯТааГЕЃЌШчВЛФмГЫЩЯЕквЛСОГЕЃЌЛЙашЫуГіФмЗёГЫЩЯгвВрЕкЖўСОЯТааГЕЃЌДгЖјЧѓГіГЫПЭДг
еОЕФЪБМфЃЌБШНЯМДПЩХаЖЯГЫПЭФмЗёГЫЩЯгвВрЕквЛСОЯТааГЕЃЌШчВЛФмГЫЩЯЕквЛСОГЕЃЌЛЙашЫуГіФмЗёГЫЩЯгвВрЕкЖўСОЯТааГЕЃЌДгЖјЧѓГіГЫПЭДг![]() ДІЕНДя
ДІЕНДя![]() еОЕФзюЩйЪБМфЃЎ
еОЕФзюЩйЪБМфЃЎ
Нт:![]() ЕквЛАрЩЯааГЕЕН
ЕквЛАрЩЯааГЕЕН![]() еОгУЪБ
еОгУЪБ![]() аЁЪБЃЌ
аЁЪБЃЌ
ЕквЛАрЯТааГЕЕН![]() еОгУЪБ
еОгУЪБ![]() аЁЪБЃЛ
аЁЪБЃЛ
![]() ЩшЕквЛАрЩЯааГЕгыЕквЛАрЯТааГЕЗЂГЕtаЁЪБЯрОр
ЩшЕквЛАрЩЯааГЕгыЕквЛАрЯТааГЕЗЂГЕtаЁЪБЯрОр![]() ЧЇУзЃЎ
ЧЇУзЃЎ
ЂйЯргіЧА:
![]() ЃЎ
ЃЎ
НтЕУ![]()
ЂкЯргіКѓ:
![]()
НтЕУ![]()
Д№:ЕквЛАрЩЯааГЕгыЕквЛАрЯТааГЕЗЂГЕКѓ![]() аЁЪБЛђ
аЁЪБЛђ![]() аЁЪБЯрОр
аЁЪБЯрОр![]() ЧЇУзЃЛ
ЧЇУзЃЛ
(3)гЩЬтвтжЊЃКЭЌЪБГіЗЂЕФвЛЖдЩЯЁЂЯТааГЕЕФЮЛжУЙигк![]() жаЕуЖдГЦЃЌГЫПЭгвВрЕквЛСОЯТааГЕРы
жаЕуЖдГЦЃЌГЫПЭгвВрЕквЛСОЯТааГЕРы![]() еОвВЪЧ
еОвВЪЧ![]() ЧЇУзЃЌетСОЯТааГЕРы
ЧЇУзЃЌетСОЯТааГЕРы![]() еОЪЧ
еОЪЧ![]() ЧЇУзЃЎ
ЧЇУзЃЎ
ЂйШє![]() ЧЇУзЃЌ
ЧЇУзЃЌ
ГЫПЭДг![]() ДІзпЕН
ДІзпЕН![]() еОЕФЪБМф
еОЕФЪБМф![]() (аЁЪБ)ЃЌ
(аЁЪБ)ЃЌ
ГЫПЭгвВрЕквЛСОЯТааГЕЕНДя![]() еОЕФЪБМф
еОЕФЪБМф![]() (аЁЪБ)ЃЌ
(аЁЪБ)ЃЌ
![]()
![]() ГЫПЭФмГЫЩЯгвВрЕквЛСОЯТааГЕЃЎ
ГЫПЭФмГЫЩЯгвВрЕквЛСОЯТааГЕЃЎ
![]() (Зжжг)
(Зжжг)
Д№:Шє![]() ЧЇУзЃЌГЫПЭДг
ЧЇУзЃЌГЫПЭДг![]() ДІЕНДя
ДІЕНДя![]() еОЕФЪБМфзюЩйвЊ
еОЕФЪБМфзюЩйвЊ![]() ЗжжгЃЎ
ЗжжгЃЎ
ЂкШє![]() ЧЇУзЃЌ
ЧЇУзЃЌ
ГЫПЭДг![]() ДІзпЕН
ДІзпЕН![]() еОЕФЪБМф
еОЕФЪБМф![]() (аЁЪБ)ЃЌ
(аЁЪБ)ЃЌ
ГЫПЭгвВрЕквЛСОЯТааГЕЕНДя![]() еОЕФЪБМф
еОЕФЪБМф![]() (аЁЪБ)ЃЌ
(аЁЪБ)ЃЌ
![]()
![]() ГЫПЭВЛФмГЫЩЯгвВрЕквЛСОЯТааГЕЃЌ
ГЫПЭВЛФмГЫЩЯгвВрЕквЛСОЯТааГЕЃЌ
![]()
![]() ГЫПЭФмГЫЩЯгвВрЕкЖўСОЯТааГЕЃЎ
ГЫПЭФмГЫЩЯгвВрЕкЖўСОЯТааГЕЃЎ
![]() (Зжжг)
(Зжжг)
Д№:Шє![]() ЧЇУзЃЌГЫПЭДг
ЧЇУзЃЌГЫПЭДг![]() ДІЕНДя
ДІЕНДя![]() еОЕФЪБМфзюЩйвЊ
еОЕФЪБМфзюЩйвЊ![]() ЗжжгЃЎ
ЗжжгЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛДЮЪ§бЇПЮЩЯЃЌРЯЪІдкЦСФЛЩЯГіЪОСЫвЛИіР§ЬтЃКдкЁїABCжаЃЌDЃЌEЗжБ№ЪЧABЃЌACЩЯЕФвЛЕуЃЌBEгыCDНЛгкЕуOЃЌЛГіЭМаЮЃЈШчЭМЃЉЃЌИјГіЯТСаЫФИіЬѕМўЃКЂйЁЯDBO=ЁЯECOЃЛЂкЁЯBDO=ЁЯCEOЃЛЂлBD=CEЃЛЂмOB=OCЃЎ
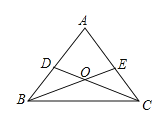
ЃЈ1ЃЉвЊЧѓЭЌбЇДгетЫФИіЕШЪНжабЁГіСНИізїЮЊвбжЊЬѕМўЃЌПЩХаЖЈЁїABCЪЧЕШбќШ§НЧаЮЃЎ
ЧыФугУађКХдкКсЯпЩЯаДГіЫљгаЧщаЮЃЎД№ЃК
ЃЈ2ЃЉбЁдёЕкЃЈ1ЃЉЬтжаЕФвЛжжЧщаЮЃЌЫЕУїЁїABCЪЧЕШбќШ§НЧаЮЕФРэгЩЃЌВЂаДГіНтЬтЙ§ГЬЃЎ
НтЃКЮвбЁдё ЃЎ
жЄУїЃК
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
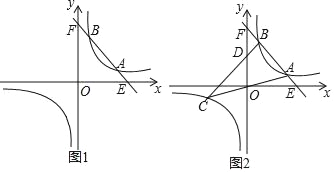
ЁОЬтФПЁПвбжЊЃКвЛДЮКЏЪ§y=Љ2x+10ЕФЭМЯѓгыЗДБШР§КЏЪ§y=![]() ЃЈkЃО0ЃЉЕФЭМЯѓЯрНЛгкAЁЂBСНЕуЃЈAЕФBЕФгвВрЃЉЃЎ
ЃЈkЃО0ЃЉЕФЭМЯѓЯрНЛгкAЁЂBСНЕуЃЈAЕФBЕФгвВрЃЉЃЎ
ЃЈ1ЃЉЕБAЃЈ4ЃЌ2ЃЉЪБЃЌЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃК
ЃЈ2ЃЉЕБAЕФКсзјБъЪЧ3ЃЌBЕФКсзјБъЪЧ2ЪБЃЌжБЯпOAгыДЫЗДБШР§КЏЪ§ЭМЯѓЕФСэвЛжЇНЛгкСэвЛЕуCЃЌСЌНгBCНЛyжсгкЕуDЃЎ
ЂйЧѓCЕуЕФзјБъЃЛ
ЂкЧѓDЕуЕФзјБъЃЛ
ЂлЧѓЁїABCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЪЧИљОнФГЪа2014ФъжС2018ФъЙЄвЕЩњВњзмжЕЛцжЦЕФелЯпЭГМЦЭМЃЌЙлВьЭГМЦЭМЛёЕУвдЯТаХЯЂЃЌЦфжаХаЖЯДэЮѓЕФЪЧЃЈ ЃЉ
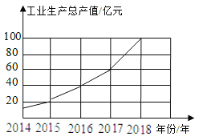
A.2014ФъжС2018ФъЙЄвЕЩњВњзмжЕж№ФъдіМг
B.2018ФъЕФЙЄвЕЩњВњзмжЕБШЧАвЛФъдіМгСЫ![]() вкдЊ
вкдЊ
C.2016Фъгы2017ФъУПвЛФъгыЧАвЛФъБШЃЌЦфдіГЄЖюЯрЭЌ
D.2015ФъжС2018ФъЃЌУПвЛФъгыЧАвЛФъБШЃЌ2018ФъЕФдіГЄТЪзюДѓ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
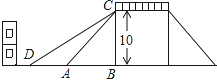
ЁОЬтФПЁПШчЭМЪЧвЛзљШЫааЬьЧХЕФЪОвтЭМЃЌЬьЧХЕФИпЖШЪЧ10УзЃЌCBЁЭDBЃЌЦТУцACЕФЧуаБНЧЮЊ45ЁуЃЎЮЊСЫЗНБуааШЫЭЦГЕЙ§ЬьЧХЃЌЪаеўВПУХОіЖЈНЕЕЭЦТЖШЃЌЪЙаТЦТУцDCЕФЦТЖШЮЊi=![]() ЃК3ЃЎШєаТЦТНЧЯТашСє3УзПэЕФШЫааЕРЃЌЮЪРыдЦТНЧЃЈAЕуДІЃЉ10УзЕФНЈжўЮяЪЧЗёашвЊВ№Г§ЃПЃЈВЮПМЪ§ОнЃК
ЃК3ЃЎШєаТЦТНЧЯТашСє3УзПэЕФШЫааЕРЃЌЮЪРыдЦТНЧЃЈAЕуДІЃЉ10УзЕФНЈжўЮяЪЧЗёашвЊВ№Г§ЃПЃЈВЮПМЪ§ОнЃК ![]() Ёж1.414ЃЌ
Ёж1.414ЃЌ ![]() Ёж1.732ЃЉ
Ёж1.732ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФЖдНЧЯпACЃЌBDЯрНЛгкЕуOЃЌНЋBDЯђСНИіЗНЯђбгГЄЃЌЗжБ№жСЕуEКЭЕуFЃЌЧвЪЙBE=DFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮAECFЪЧСтаЮЃЛ
ЃЈ2ЃЉШєAC=4ЃЌBE=1ЃЌжБНгаДГіСтаЮAECFЕФБпГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAB=DBЃЌЁЯ1=ЁЯ2ЃЌЧыЮЪЬэМгЯТУцФФИіЬѕМўВЛФмХаЖЯЁїABCЁеЁїDBEЕФЪЧЃЈЁЁЁЁЃЉ

A. BC=BE B. ЁЯA=ЁЯD C. ЁЯACB=ЁЯDEB D. AC=DE
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§жсЩЯЕу![]() гыЕу
гыЕу![]() жЎМфЕФОрЕФОрРыЮЊ
жЎМфЕФОрЕФОрРыЮЊ![]() ИіЕЅЮЛГЄЖШЃЌЕу
ИіЕЅЮЛГЄЖШЃЌЕу![]() дкдЕуЕФзѓВрЃЌЕНдЕуЕФОрРыЮЊ
дкдЕуЕФзѓВрЃЌЕНдЕуЕФОрРыЮЊ![]() ИіЕЅЮЛГЄЖШЃЌЕу
ИіЕЅЮЛГЄЖШЃЌЕу![]() дкЕу
дкЕу![]() ЕФгвВрЃЌЕу
ЕФгвВрЃЌЕу![]() БэЪОЕФЪ§гыЕу
БэЪОЕФЪ§гыЕу![]() БэЪОЕФЪ§ЛЅЮЊЯрЗДЪ§ЃЌЖЏЕу
БэЪОЕФЪ§ЛЅЮЊЯрЗДЪ§ЃЌЖЏЕу![]() Дг
Дг![]() ЕуГіЗЂЃЌвдУПУы
ЕуГіЗЂЃЌвдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕу
ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕу![]() вЦЖЏЃЌЩшвЦЖЏЪБМфЮЊ
вЦЖЏЃЌЩшвЦЖЏЪБМфЮЊ![]() УыЃЎ
УыЃЎ
ЃЈ1ЃЉЕу![]() БэЪОЕФЪ§ЮЊ ЃЌЕу
БэЪОЕФЪ§ЮЊ ЃЌЕу![]() БэЪОЕФЪ§ЮЊ ЃЌЕу
БэЪОЕФЪ§ЮЊ ЃЌЕу![]() БэЪОЕФЪ§ЮЊ ЃЎ
БэЪОЕФЪ§ЮЊ ЃЎ
ЃЈ2ЃЉгУКЌ![]() ЕФДњЪ§ЪНЗжБ№БэЪОЕу
ЕФДњЪ§ЪНЗжБ№БэЪОЕу![]() ЕНЕу
ЕНЕу![]() КЭЕу
КЭЕу![]() ЕФОрРыЃК
ЕФОрРыЃК![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЕБЕу![]() дЫЖЏЕН
дЫЖЏЕН![]() ЕуЪБЃЌЕу
ЕуЪБЃЌЕу![]() Дг
Дг![]() ЕуГіЗЂЃЌвдУПУы
ЕуГіЗЂЃЌвдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШЯђ
ИіЕЅЮЛГЄЖШЕФЫйЖШЯђ![]() ЕудЫЖЏЃЌЕу
ЕудЫЖЏЃЌЕу![]() ЕНДя
ЕНДя![]() ЕуКѓЃЌСЂМДвдЭЌбљЕФЫйЖШЗЕЛиЕу
ЕуКѓЃЌСЂМДвдЭЌбљЕФЫйЖШЗЕЛиЕу![]() ЃЌдкЕу
ЃЌдкЕу![]() ПЊЪМдЫЖЏКѓЃЌЕБ
ПЊЪМдЫЖЏКѓЃЌЕБ![]() СНЕужЎМфЕФОрРыЮЊ
СНЕужЎМфЕФОрРыЮЊ![]() ИіЕЅЮЛГЄЖШЪБЃЌЧѓДЫЪБЕу
ИіЕЅЮЛГЄЖШЪБЃЌЧѓДЫЪБЕу![]() БэЪОЕФЪ§ЃЎ
БэЪОЕФЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊБп
ЮЊБп![]() ЩЯвЛЖЏЕуЃЌ
ЩЯвЛЖЏЕуЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() ЕФзюаЁжЕЮЊЃЈ ЃЉ
ЕФзюаЁжЕЮЊЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com