
【题目】在一次数学课上,老师在屏幕上出示了一个例题:在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,画出图形(如图),给出下列四个条件:①∠DBO=∠ECO;②∠BDO=∠CEO;③BD=CE;④OB=OC.
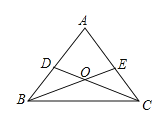
(1)要求同学从这四个等式中选出两个作为已知条件,可判定△ABC是等腰三角形.
请你用序号在横线上写出所有情形.答:
(2)选择第(1)题中的一种情形,说明△ABC是等腰三角形的理由,并写出解题过程.
解:我选择 .
证明:
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是数轴上的三点,点
是数轴上的三点,点![]() 表示的数是6,
表示的数是6,![]() .
.
![]()
(1)写出数轴上点![]() ,点
,点![]() 表示的数;
表示的数;
(2)点![]() 为线段
为线段![]() 的中点,
的中点,![]() ,求
,求![]() 的长;
的长;
(3)动点![]() 分别从
分别从![]() 同时出发,点
同时出发,点![]() 以每秒6个单位长度的速度沿数轴向右匀速运动,点
以每秒6个单位长度的速度沿数轴向右匀速运动,点![]() 以每秒3个单位长度的速度沿数轴向左匀速运动,求
以每秒3个单位长度的速度沿数轴向左匀速运动,求![]() 为何值时,原点
为何值时,原点![]() 恰好为线段
恰好为线段![]() 的中点.
的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,正方形![]() 的边长为
的边长为![]() ,动点
,动点![]() 从点
从点![]() 出发,在正方形的边上沿
出发,在正方形的边上沿![]() 运动,设运动的时间为
运动,设运动的时间为![]() ,点
,点![]() 移动的路程为
移动的路程为![]() ,
,![]() 与
与![]() 的函数图象如图②,请回答下列问题:
的函数图象如图②,请回答下列问题:

(1)点![]() 在
在![]() 上运动的时间为
上运动的时间为 ![]() ,在
,在![]() 上运动的速度为
上运动的速度为 ![]()
(2)设![]() 的面积为
的面积为![]() ,求当点
,求当点![]() 在
在![]() 上运动时,
上运动时,![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
(3)①下列图表示![]() 的面积
的面积![]() 与时间
与时间![]() 之间的函数图象是 .
之间的函数图象是 .
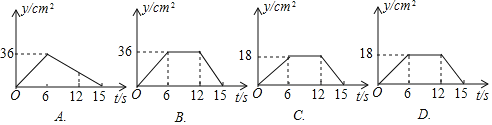
②当![]()
![]() 时,
时,![]() 的面积为
的面积为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
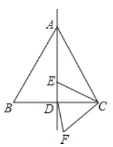
【题目】如图,边长为4的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF,则在点E运动过程中,DF的最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
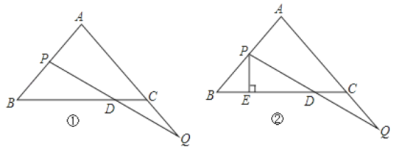
【题目】如图,等边△ABC的边长为6,点P从点B出发沿射线BA移动,同时,点Q从点C出发沿线段AC的延长线移动,已知点P、Q移动的速度相同,PQ与直线BC相交于点D.
(1)如图①,当点P为AB的中点时,求CD的长;
(2)如图②,过点P作直线BC的垂线,垂足为E,当点P、Q在移动的过程中,线段BE、DE、CD中是否存在长度保持不变的线段?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(理解新知)如图①,已知![]() ,在
,在![]() 内部画射线
内部画射线![]() ,得到三个角,分别为
,得到三个角,分别为![]() ,
,![]() ,
,![]() ,若这三个角中有一个角是另外一个角的两倍,则称射线
,若这三个角中有一个角是另外一个角的两倍,则称射线![]() 为
为![]() 的“二倍角线”.
的“二倍角线”.
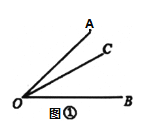
(1)一个角的角平分线______这个角的“二倍角线”(填“是”或“不是”)
(2)若![]() ,射线
,射线![]() 为
为![]() 的“二倍角线”,则
的“二倍角线”,则![]() 的大小是______;
的大小是______;
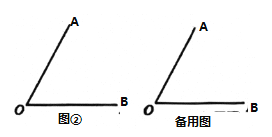
(解决问题)如图②,己知![]() ,射线
,射线![]() 从
从![]() 出发,以
出发,以![]() /秒的速度绕
/秒的速度绕![]() 点逆时针旋转;射线
点逆时针旋转;射线![]() 从
从![]() 出发,以
出发,以![]() /秒的速度绕
/秒的速度绕![]() 点顺时针旋转,射线
点顺时针旋转,射线![]() ,
,![]() 同时出发,当其中一条射线回到出发位置的时候,整个运动随之停止,设运动的时间为
同时出发,当其中一条射线回到出发位置的时候,整个运动随之停止,设运动的时间为![]() 秒.
秒.
(3)当射线![]() ,
,![]() 旋转到同一条直线上时,求
旋转到同一条直线上时,求![]() 的值;
的值;
(4)若![]() ,
,![]() ,
,![]() 三条射线中,一条射线恰好是以另外两条射线为边组成的角的“二倍角线”,直接写出
三条射线中,一条射线恰好是以另外两条射线为边组成的角的“二倍角线”,直接写出![]() 所有可能的值______.
所有可能的值______.
查看答案和解析>>
科目:初中数学 来源: 题型:
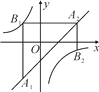
【题目】如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-![]() 上,并且满足A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2018=_______.
上,并且满足A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2018=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公共汽车行驶在笔直的公路上,这条路上有![]() 四个站点,每相邻两站之间的距离为
四个站点,每相邻两站之间的距离为![]() 千米,从
千米,从![]() 站开往
站开往![]() 站的车称为上行车,从
站的车称为上行车,从![]() 站开往
站开往![]() 站的车称为下行车.第一班上行车、下行车分别从
站的车称为下行车.第一班上行车、下行车分别从![]() 站、
站、![]() 站同时发车,相向而行,且以后上行车、下行车每隔
站同时发车,相向而行,且以后上行车、下行车每隔![]() 分钟分别在
分钟分别在![]() 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、 下行车的速度均为
站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、 下行车的速度均为![]() 千米/小时.
千米/小时.
![]() 第一班上行车到
第一班上行车到![]() 站、第一班下行车到
站、第一班下行车到![]() 站分别用时多少?
站分别用时多少?
![]() 第一班上行车与第一班下行车发车后多少小时相距
第一班上行车与第一班下行车发车后多少小时相距![]() 千米?
千米?
![]() 一乘客在
一乘客在![]() 两站之间的
两站之间的![]() 处,刚好遇到上行车,
处,刚好遇到上行车,![]() 千米,他从
千米,他从![]() 处以
处以![]() 千米/小时的速度步行到
千米/小时的速度步行到![]() 站乘下行车前往
站乘下行车前往![]() 站办事.
站办事.

①若![]() 千米,乘客从
千米,乘客从![]() 处到达
处到达![]() 站的时间最少要几分钟?
站的时间最少要几分钟?
②若![]() 千米,乘客从
千米,乘客从![]() 处到达
处到达![]() 站的时间最少要几分钟?
站的时间最少要几分钟?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com