
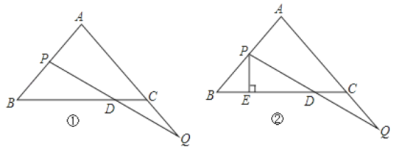
【题目】如图,等边△ABC的边长为6,点P从点B出发沿射线BA移动,同时,点Q从点C出发沿线段AC的延长线移动,已知点P、Q移动的速度相同,PQ与直线BC相交于点D.
(1)如图①,当点P为AB的中点时,求CD的长;
(2)如图②,过点P作直线BC的垂线,垂足为E,当点P、Q在移动的过程中,线段BE、DE、CD中是否存在长度保持不变的线段?请说明理由.
【答案】(1)![]() ;(2)线段ED的长度保持不变.
;(2)线段ED的长度保持不变.
【解析】
(1)过P点作PF//AC交BC于F,由题意可证△BPF是等边三角形,△PFD≌△QCD,即可求CD的长;
(2)分点P在线段AB上,点P在线段BA的延长线上两种情况讨论,利用全等三角形的性质和判定可得DE的长度不变.
解:(1)如图,过P点作PF∥AC交BC于F,
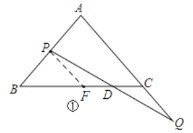
∵点P和点Q同时出发,且速度相同,
∴BP=CQ,
∵PF∥AQ,
∴∠PFB=∠ACB=60°,∠DPF=∠CQD,
又∵AB=AC,
∴∠B=∠ACB,∴∠B=∠PFB,
∴BP=PF,
∴PF=CQ,又∠PDF=∠QDC,
∴△PFD≌△QCD,且△PBF是等边三角形
∴![]() ,BF=PB
,BF=PB
∵P是AB的中点,即![]() ,
,
∴BF=3
∴![]() ;
;
(2)分两种情况讨论,得ED为定值,是不变的线段
如图,如果点P在线段AB上,
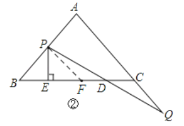
过点P作PF∥AC交BC于F,
由(1)证得△PFD≌△QCD,且△PBF是等边三角形
∴![]()
∴![]()
∴ED为定值
同理,如图,若P在BA的延长线上,
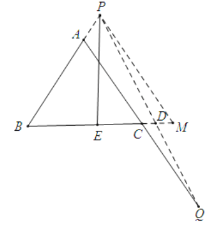
作PM∥AC的延长线于M,
∴∠PMC=∠ACB,又∵AB=AC,
∴∠B=∠ACB=60°,
∴∠B=∠PMC=60°,
∴PM=PB,且PE⊥BC
∴![]() ,△PBM是等边三角形
,△PBM是等边三角形
∴PM=PB=CQ
∵PM∥AC
∴∠PMB=∠QCM,∠MPD=∠CQD且PM=CQ
∴△PMD≌△QCD(ASA),
∴![]() ,
,
∴![]()
综上所述,线段ED的长度保持不变.


科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,图①是沿
的中点,图①是沿![]() 将
将![]() 折叠,点
折叠,点![]() 落在
落在![]() 上,图②是绕点
上,图②是绕点![]() 将
将![]() 顺时针旋转
顺时针旋转![]() .
.
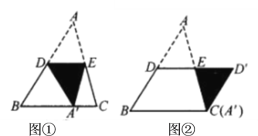
(1)在图①中,判断![]() 和
和![]() 形状.(填空)_______________________________________
形状.(填空)_______________________________________
(2)在图②中,判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象经过![]() ,
,![]() 两点.
两点.
(1)求这个一次函数的解析式;
(2)试判断点![]() 是否在这个一次函数的图象上;
是否在这个一次函数的图象上;
(3)求此函数图象与![]() 轴,
轴,![]() 轴围成的三角形的面积.
轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】华联超市第一次用7000元购进甲、乙两种商品,其中甲商品的件数是乙商品件数的2倍,甲、乙两种商品的进价和售价如表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 25 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍:甲商品按原价销售,乙商品打折销售,第二次两种商品都售完以后获得的总利润比第一次获得的总利润多800元,求第二次乙商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,老师在屏幕上出示了一个例题:在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,画出图形(如图),给出下列四个条件:①∠DBO=∠ECO;②∠BDO=∠CEO;③BD=CE;④OB=OC.
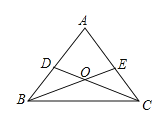
(1)要求同学从这四个等式中选出两个作为已知条件,可判定△ABC是等腰三角形.
请你用序号在横线上写出所有情形.答:
(2)选择第(1)题中的一种情形,说明△ABC是等腰三角形的理由,并写出解题过程.
解:我选择 .
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把一根细线绳对折成两条重合的线段![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.

(l)若细线绳的长度是![]() ,求图中线段
,求图中线段![]() 的长;
的长;
(2)从点![]() 处把细线绳剪断后展开,细线绳变成三段,若三段中最长的一段为
处把细线绳剪断后展开,细线绳变成三段,若三段中最长的一段为![]() ,求原来细线绳的长.
,求原来细线绳的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平面内两点![]() .
.

(1)请用尺规按下列要求作图,并保留作图痕迹;
①连接![]() ;
;
②在线段![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() ;
;
③在线段![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() .
.
(2)请求出线段![]() 与线段
与线段![]() 长度之间的数量关系.
长度之间的数量关系.
(3)如果![]() ,则
,则![]() 的长度为________,
的长度为________,![]() 的长度为________,
的长度为________,![]() 的长度为_________.
的长度为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)求证:四边形AECF是菱形;
(2)若AC=4,BE=1,直接写出菱形AECF的边长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com