
【题目】如图,已知平面内两点![]() .
.

(1)请用尺规按下列要求作图,并保留作图痕迹;
①连接![]() ;
;
②在线段![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() ;
;
③在线段![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() .
.
(2)请求出线段![]() 与线段
与线段![]() 长度之间的数量关系.
长度之间的数量关系.
(3)如果![]() ,则
,则![]() 的长度为________,
的长度为________,![]() 的长度为________,
的长度为________,![]() 的长度为_________.
的长度为_________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】数学课上,同学们遇到这样一个问题:
如图1,已知![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 与
与 ![]() 的角平分线,请同学们根据题中的条件提出问题,大家一起来解决(本题出现的角均小于平角)
的角平分线,请同学们根据题中的条件提出问题,大家一起来解决(本题出现的角均小于平角)
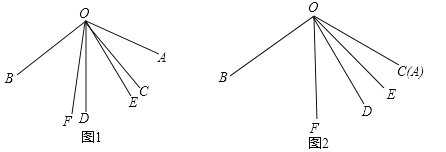
同学们经过思考后,交流了自己的想法:
小强说:“如图2,若![]() 与
与![]() 重合,且
重合,且![]() ,
,![]() 时,可求
时,可求![]() 的度数.”
的度数.”
小伟说:“在小强提出问題的前提条件下,将![]() 的
的![]() 边从
边从![]() 边开始绕点
边开始绕点![]() 逆时针
逆时针
转动![]() ,可求出
,可求出![]() 的值.”
的值.”
老师说:“在原題的条件下,借助射线![]() 的不同位置可得出的数量关系.”
的不同位置可得出的数量关系.”
(1)请解决小强提出的问题;
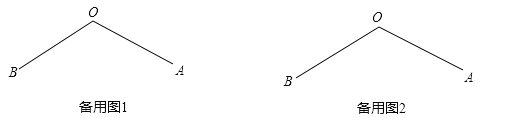
(2)在备用图1中,补充完整的图形,并解决小伟提出的问题
(3)在备用图2中,补充完整的图形,并解决老师提出的问题,即求![]() 三者之间的的数量关系.
三者之间的的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,正方形![]() 的边长为
的边长为![]() ,动点
,动点![]() 从点
从点![]() 出发,在正方形的边上沿
出发,在正方形的边上沿![]() 运动,设运动的时间为
运动,设运动的时间为![]() ,点
,点![]() 移动的路程为
移动的路程为![]() ,
,![]() 与
与![]() 的函数图象如图②,请回答下列问题:
的函数图象如图②,请回答下列问题:

(1)点![]() 在
在![]() 上运动的时间为
上运动的时间为 ![]() ,在
,在![]() 上运动的速度为
上运动的速度为 ![]()
(2)设![]() 的面积为
的面积为![]() ,求当点
,求当点![]() 在
在![]() 上运动时,
上运动时,![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
(3)①下列图表示![]() 的面积
的面积![]() 与时间
与时间![]() 之间的函数图象是 .
之间的函数图象是 .
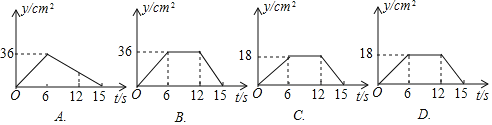
②当![]()
![]() 时,
时,![]() 的面积为
的面积为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
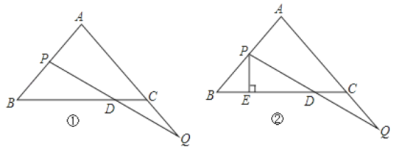
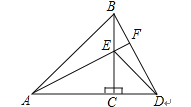
【题目】如图,等边△ABC的边长为6,点P从点B出发沿射线BA移动,同时,点Q从点C出发沿线段AC的延长线移动,已知点P、Q移动的速度相同,PQ与直线BC相交于点D.
(1)如图①,当点P为AB的中点时,求CD的长;
(2)如图②,过点P作直线BC的垂线,垂足为E,当点P、Q在移动的过程中,线段BE、DE、CD中是否存在长度保持不变的线段?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(理解新知)如图①,已知![]() ,在
,在![]() 内部画射线
内部画射线![]() ,得到三个角,分别为
,得到三个角,分别为![]() ,
,![]() ,
,![]() ,若这三个角中有一个角是另外一个角的两倍,则称射线
,若这三个角中有一个角是另外一个角的两倍,则称射线![]() 为
为![]() 的“二倍角线”.
的“二倍角线”.
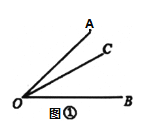
(1)一个角的角平分线______这个角的“二倍角线”(填“是”或“不是”)
(2)若![]() ,射线
,射线![]() 为
为![]() 的“二倍角线”,则
的“二倍角线”,则![]() 的大小是______;
的大小是______;
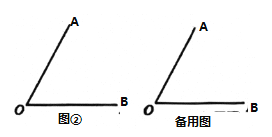
(解决问题)如图②,己知![]() ,射线
,射线![]() 从
从![]() 出发,以
出发,以![]() /秒的速度绕
/秒的速度绕![]() 点逆时针旋转;射线
点逆时针旋转;射线![]() 从
从![]() 出发,以
出发,以![]() /秒的速度绕
/秒的速度绕![]() 点顺时针旋转,射线
点顺时针旋转,射线![]() ,
,![]() 同时出发,当其中一条射线回到出发位置的时候,整个运动随之停止,设运动的时间为
同时出发,当其中一条射线回到出发位置的时候,整个运动随之停止,设运动的时间为![]() 秒.
秒.
(3)当射线![]() ,
,![]() 旋转到同一条直线上时,求
旋转到同一条直线上时,求![]() 的值;
的值;
(4)若![]() ,
,![]() ,
,![]() 三条射线中,一条射线恰好是以另外两条射线为边组成的角的“二倍角线”,直接写出
三条射线中,一条射线恰好是以另外两条射线为边组成的角的“二倍角线”,直接写出![]() 所有可能的值______.
所有可能的值______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴快车是一种便捷的出行工具,分为普通快车和优享型快车;两种.下表是普通快车的收费标准:
计费项目 | 起步价 | 里程费 | 时长费 | 远途费 |
计费价格 | 8 | 2.0元/公里 | 0.4元/分 | 1.0元/公里 |
注:车费由起步价、里程费、时长费、远途费四部分组成,其中起步价包含里程2公里,时长5分钟;里程 | ||||
(1)张敏乘坐滴滴普通快车,行车里程7公里,行车时间15分钟,求张敏下车时付多少车费?
(2)王红乘坐滴滴普通快车,行车里程22公里,下车时所付车费63.4元,则这辆滴滴快车的行车时间为多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
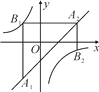
【题目】如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-![]() 上,并且满足A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2018=_______.
上,并且满足A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2018=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点.
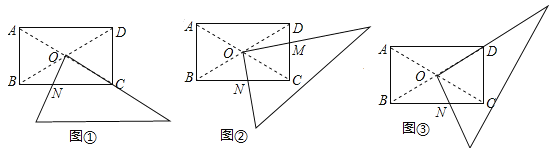
(1)该学习小组成员意外的发现图①中(三角板一边与CC重合),BN、CN、CD这三条线段之间存在一定的数量关系:CN2=BN2+CD2,请你对这名成员在图①中发现的结论说明理由;
(2)在图③中(三角板一直角边与OD重合),试探究图③中BN、CN、CD这三条线段之间的数量关系,直接写出你的结论.
(3)试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如 图,△ACB和△E CD都是等腰直角三角形,A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于F.
(1)求证:△ACE≌△BCD;
(2)直线AE与BD互相垂直吗?请证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com