
����Ŀ����������֪����ͼ�٣���֪![]() ����
����![]() �ڲ�������
�ڲ�������![]() ���õ������ǣ��ֱ�Ϊ
���õ������ǣ��ֱ�Ϊ![]() ��
��![]() ��
��![]() ����������������һ����������һ���ǵ��������������
����������������һ����������һ���ǵ��������������![]() Ϊ
Ϊ![]() �ġ��������ߡ���
�ġ��������ߡ���
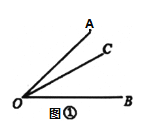
��1��һ���ǵĽ�ƽ����______����ǵġ��������ߡ�����ǡ����ǡ���
��2����![]() ������
������![]() Ϊ
Ϊ![]() �ġ��������ߡ�����
�ġ��������ߡ�����![]() �Ĵ�С��______��
�Ĵ�С��______��
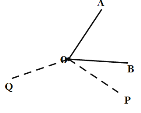
��������⣩��ͼ�ڣ���֪![]() ������
������![]() ��
��![]() ��������
��������![]() /����ٶ���
/����ٶ���![]() ����ʱ����ת������
����ʱ����ת������![]() ��
��![]() ��������
��������![]() /����ٶ���
/����ٶ���![]() ��˳ʱ����ת������
��˳ʱ����ת������![]() ��
��![]() ͬʱ������������һ�����ص�����λ�õ�ʱ�������˶���ֹ֮ͣ�����˶���ʱ��Ϊ
ͬʱ������������һ�����ص�����λ�õ�ʱ�������˶���ֹ֮ͣ�����˶���ʱ��Ϊ![]() �룮
�룮
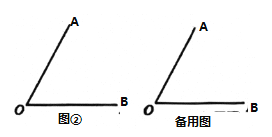
��3��������![]() ��
��![]() ��ת��ͬһ��ֱ����ʱ����
��ת��ͬһ��ֱ����ʱ����![]() ��ֵ��
��ֵ��
��4����![]() ��
��![]() ��
��![]() ���������У�һ������ǡ������������������Ϊ����ɵĽǵġ��������ߡ���ֱ��д��
���������У�һ������ǡ������������������Ϊ����ɵĽǵġ��������ߡ���ֱ��д��![]() ���п��ܵ�ֵ______��
���п��ܵ�ֵ______��
���𰸡���1���ǣ���2��![]() ��
��![]() ��
��![]() ����3��
����3��![]() ��
��![]() ��
��![]() ����4��
����4��![]() ��
��![]() .
.
��������
��1����OCΪ![]() �Ľ�ƽ���ߣ��ɽ�ƽ���ߵĶ���ɵ�
�Ľ�ƽ���ߣ��ɽ�ƽ���ߵĶ���ɵ�![]() ���ɶ������ߵĶ����֪���ۣ�
���ɶ������ߵĶ����֪���ۣ�
��2�����ݶ������ߵĶ����![]() ����������
����������![]() �Ĵ�С����.
�Ĵ�С����.
��3��������![]() ��
��![]() ��ת��ͬһ��ֱ����ʱ��
��ת��ͬһ��ֱ����ʱ��![]() ����
����![]() ��
��![]() ����OP��OQ�غ�ʱ����
����OP��OQ�غ�ʱ����![]() ���ú�t��ʽ�ӱ�ʾ��OP��OQ��ת�ĽǶȴ����������������⼴�ɣ�
���ú�t��ʽ�ӱ�ʾ��OP��OQ��ת�ĽǶȴ����������������⼴�ɣ�
��4����ϡ��������ߡ��Ķ��壬����t��ȡֵ��Χ��![]() ��
��![]() ��
��![]() ��
��![]() 4��������ۼ���.
4��������ۼ���.
�⣺��1����OCΪ![]() �Ľ�ƽ���ߣ��ɽ�ƽ���ߵĶ���ɵ�
�Ľ�ƽ���ߣ��ɽ�ƽ���ߵĶ���ɵ�![]() ���ɶ������ߵĶ����֪һ���ǵĽ�ƽ����������ǵġ��������ߡ���
���ɶ������ߵĶ����֪һ���ǵĽ�ƽ����������ǵġ��������ߡ���
��2��������![]() Ϊ
Ϊ![]() �ġ��������ߡ�ʱ����3�������
�ġ��������ߡ�ʱ����3�������
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
�ۺ�������![]() �Ĵ�СΪ
�Ĵ�СΪ![]() ��
��![]() ��
��![]() ��
��
��3��������![]() ��
��![]() ��ת��ͬһ��ֱ����ʱ��������3�������
��ת��ͬһ��ֱ����ʱ��������3�������
����ͼ
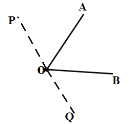
��ʱ![]() ����
����![]() �����
�����![]() ��
��
����ͼ
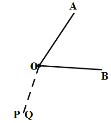
��ʱ��P�͵�Q�غϣ��ɵ�![]() ����
����![]() �����
�����![]() ��
��
����ͼ
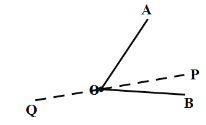
��ʱ![]() ����
����![]() �����
�����![]() ��
��
�ۺ�������![]() ��
��![]() ��
��![]() ��
��
��4���������˶�ֹͣʱ![]() ������
������![]() ��
��
�ٵ�![]() ʱ����ͼ��
ʱ����ͼ��
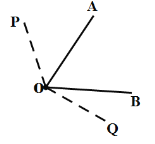
��ʱOAΪ![]() �����������ߡ���
�����������ߡ���![]() ��
��
��![]() �����
�����![]() ��
��
����![]() ʱ����ͼ��
ʱ����ͼ��
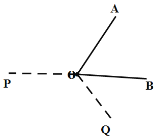
��ʱ��![]() �����Բ����ڣ�
�����Բ����ڣ�
�۵�![]() ʱ����ͼ
ʱ����ͼ
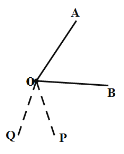
��ʱOPΪ![]() �ġ��������ߡ���
�ġ��������ߡ���![]() ��
��
��![]()
��� ![]() ��
��
����![]() ʱ����ͼ��
ʱ����ͼ��
��ʱ![]() �����Բ����ڣ�
�����Բ����ڣ�
������������![]() ��
��![]() ʱ��
ʱ��![]() ��
��![]() ��
��![]() ���������У�һ������ǡ������������������Ϊ����ɵĽǵġ��������ߡ�.
���������У�һ������ǡ������������������Ϊ����ɵĽǵġ��������ߡ�.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
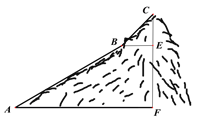
����Ŀ����ͼ��Ϊ����һ��ɽ��CF�ĸ߶ȣ�����ɽ��ij��ɽ�»���ΪAB��BC���Σ�ÿһ��ɽ�½����ǡ�ֱ���ģ�����³�AB=800�ף�BC=200�ף�б��AB���¶�![]() �����ǡ�CBE=50��.��ɽ��ĸ߶�CFԼΪ�� ����.�����õIJο����ݣ�sin50���0.8��tan50���1.2,
�����ǡ�CBE=50��.��ɽ��ĸ߶�CFԼΪ�� ����.�����õIJο����ݣ�sin50���0.8��tan50���1.2, ![]() ��
��
A. 500 B. 518 C. 530 D. 580
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�˿�ѧ������ѧ�������ɳ��������������ȡ�˲���ѧ����ͥ����ҳ�����������Ϊ����ĩ�����ڼ��������������ʾ����飬�����յ��ʾ����з����������õ������µ�����ͳ�Ʊ�������ͳ��ͼ��
���� | ������� | ��ͥ�� |
| �������沢�ҹ�������ҵ������ | 16 |
| ֻ��������ҵ������ | b |
| ֻ�������� | 8 |
| �Ȳ���������Ҳ����������ҵ������ | d |
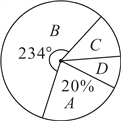
��1����![]() ��ֵ��
��ֵ��
��2����Уѧ����ͥ����Ϊ500��ѧУ������������![]() ���ͥ�г�ȡ�ҳ������ѵ�࣬�����Ϊ
���ͥ�г�ȡ�ҳ������ѵ�࣬�����Ϊ![]() ��ȡ20%��
��ȡ20%��![]() ���ȡ60%��������Ƹ���ѵ��ļ�ͥ����
���ȡ60%��������Ƹ���ѵ��ļ�ͥ����
��3������![]() ���ͥ��ֻ��һ�������ͥ��������ũ���ͥ�������оٷ������
���ͥ��ֻ��һ�������ͥ��������ũ���ͥ�������оٷ������![]() ����������2����ͥ������Ȳɷã�������һ���dz����ͥ�ĸ��ʣ�
����������2����ͥ������Ȳɷã�������һ���dz����ͥ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ѧ���ϣ���ʦ����Ļ�ϳ�ʾ��һ�����⣺����ABC�У�D��E�ֱ���AB��AC�ϵ�һ�㣬BE��CD���ڵ�O������ͼ�Σ���ͼ�������������ĸ��������١�DBO=��ECO���ڡ�BDO=��CEO����BD=CE����OB=OC��
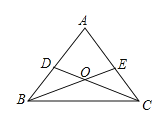
��1��Ҫ��ͬѧ�����ĸ���ʽ��ѡ��������Ϊ��֪���������ж���ABC�ǵ��������Σ�
����������ں�����д���������Σ���
��2��ѡ��ڣ�1�����е�һ�����Σ�˵����ABC�ǵ��������ε����ɣ���д��������̣�
�⣺��ѡ�� ��
֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
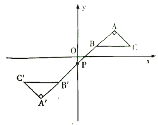
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() �Ķ���
�Ķ���![]() �ڵ�һ���ޣ���
�ڵ�һ���ޣ���![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ���ڵ�
���ڵ�![]() �����ĶԳƣ����
�����ĶԳƣ����![]() ������Ϊ�� ��
�������� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ƽ��������![]() ��
��

��1�����ó߹水����Ҫ����ͼ����������ͼ�ۼ���
������![]() ��
��
�����߶�![]() ���ӳ�����ȡ��
���ӳ�����ȡ��![]() ��ʹ
��ʹ![]() ��
��
�����߶�![]() ���ӳ�����ȡ��
���ӳ�����ȡ��![]() ��ʹ
��ʹ![]() ��
��
��2��������߶�![]() ���߶�
���߶�![]() ����֮���������ϵ��
����֮���������ϵ��
��3�����![]() ����
����![]() �ij���Ϊ________��
�ij���Ϊ________��![]() �ij���Ϊ________��
�ij���Ϊ________��![]() �ij���Ϊ_________��
�ij���Ϊ_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O���������������ж�����ı�����ƽ���ı��ε���

A��AB��DC��AD��BC����B��AB=DC��AD=BC
C��AO=CO��BO=DO�� ��D��AB��DC��AD=BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
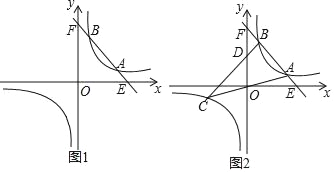
����Ŀ����֪��һ�κ���y=��2x+10��ͼ���뷴��������y=![]() ��k��0����ͼ���ཻ��A��B���㣨A��B���Ҳࣩ��
��k��0����ͼ���ཻ��A��B���㣨A��B���Ҳࣩ��
��1����A��4��2��ʱ�����������Ľ���ʽ��
��2����A�ĺ�������3��B�ĺ�������2ʱ��ֱ��OA��˷���������ͼ�����һ֧������һ��C������BC��y���ڵ�D��
����C������ꣻ
����D������ꣻ
������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB=DB����1=��2���������������ĸ����������ж���ABC�ա�DBE���ǣ�������

A. BC=BE B. ��A=��D C. ��ACB=��DEB D. AC=DE
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com