
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,斜坡AB的坡度![]() ,仰角∠CBE=50°.则山峰的高度CF约为( )米.(可用的参考数据:sin50°≈0.8,tan50°≈1.2,
,仰角∠CBE=50°.则山峰的高度CF约为( )米.(可用的参考数据:sin50°≈0.8,tan50°≈1.2, ![]() )
)
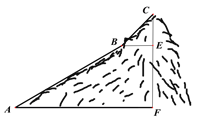
A. 500 B. 518 C. 530 D. 580
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
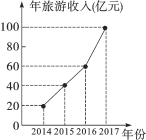
【题目】某人为了解他所在地区的旅游情况,收集了该地区2014年到2017年每年旅游收入的有关数据,整理并绘制成折线统计图,根据图中信息,回答下列问题:
(1)该地区2014年到2017年四年的年旅游平均收入是多少亿元;
(2)从折线统计图中你能获得哪些信息?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD是一块绿化带,阴影部分EOFB,GHMN都是正方形的花圃,其中EOFB的顶点O是正方形中心.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是数轴上的三点,点
是数轴上的三点,点![]() 表示的数是6,
表示的数是6,![]() .
.
![]()
(1)写出数轴上点![]() ,点
,点![]() 表示的数;
表示的数;
(2)点![]() 为线段
为线段![]() 的中点,
的中点,![]() ,求
,求![]() 的长;
的长;
(3)动点![]() 分别从
分别从![]() 同时出发,点
同时出发,点![]() 以每秒6个单位长度的速度沿数轴向右匀速运动,点
以每秒6个单位长度的速度沿数轴向右匀速运动,点![]() 以每秒3个单位长度的速度沿数轴向左匀速运动,求
以每秒3个单位长度的速度沿数轴向左匀速运动,求![]() 为何值时,原点
为何值时,原点![]() 恰好为线段
恰好为线段![]() 的中点.
的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题:(假设行车过程没有停车等时,且平均车速为0.5千米/分钟)
华夏专车 | 神州专车 | |
里程费 | 1.8元/千米 | 2元/千米 |
时长费 | 0.3元/分钟 | 0.6元/分钟 |
远途费 | 0.8元/千米产(超过7千米部分) | 无 |
起步价 | 无 | 10元 |
华夏专车:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7千米以内(含7千米)不收远途费,超过7千米的,超出的部分按每千米加收0.8元. 神州专车:车费由里程费、时长费、起步价三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;起步价与行车距离无关. | ||
(1)小明在该地区出差,乘车距离为10千米,如果小明使用华夏专车,需要支付的打车费用为 元;
(2)小强在该地区从甲地乘坐神州专车到乙地,一共花费42元,求甲乙两地距离是多少千米?
(3)神州专车为了和华夏专车竞争客户,分别推出了优惠方式,华夏专车对于乘车路程在7千米以上(含7千米)的客户每次收费立减9元;神州打车车费5折优惠.对采用哪一种打车方式更合算提出你的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,同学们遇到这样一个问题:
如图1,已知![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 与
与 ![]() 的角平分线,请同学们根据题中的条件提出问题,大家一起来解决(本题出现的角均小于平角)
的角平分线,请同学们根据题中的条件提出问题,大家一起来解决(本题出现的角均小于平角)
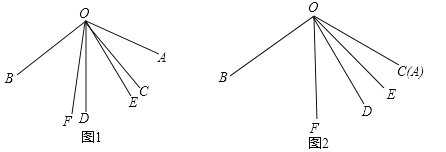
同学们经过思考后,交流了自己的想法:
小强说:“如图2,若![]() 与
与![]() 重合,且
重合,且![]() ,
,![]() 时,可求
时,可求![]() 的度数.”
的度数.”
小伟说:“在小强提出问題的前提条件下,将![]() 的
的![]() 边从
边从![]() 边开始绕点
边开始绕点![]() 逆时针
逆时针
转动![]() ,可求出
,可求出![]() 的值.”
的值.”
老师说:“在原題的条件下,借助射线![]() 的不同位置可得出的数量关系.”
的不同位置可得出的数量关系.”
(1)请解决小强提出的问题;
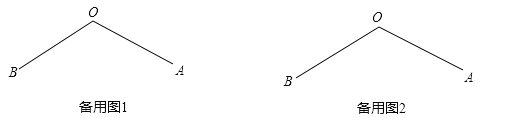
(2)在备用图1中,补充完整的图形,并解决小伟提出的问题
(3)在备用图2中,补充完整的图形,并解决老师提出的问题,即求![]() 三者之间的的数量关系.
三者之间的的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
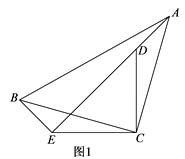
【题目】已知等腰RtABC与等腰RtCDE,∠ACB=∠DCE=90°.把RtABC绕点C旋转.
(1)如图1,当点A旋转到ED的延长线时,若![]() ,BE=5,求CD的长;
,BE=5,求CD的长;
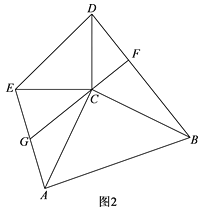
(2)当RtABC旋转到如图2所示的位置时,过点C作BD的垂线交BD于点F,交AE于点G,求证:BD=2CG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(理解新知)如图①,已知![]() ,在
,在![]() 内部画射线
内部画射线![]() ,得到三个角,分别为
,得到三个角,分别为![]() ,
,![]() ,
,![]() ,若这三个角中有一个角是另外一个角的两倍,则称射线
,若这三个角中有一个角是另外一个角的两倍,则称射线![]() 为
为![]() 的“二倍角线”.
的“二倍角线”.
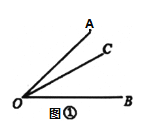
(1)一个角的角平分线______这个角的“二倍角线”(填“是”或“不是”)
(2)若![]() ,射线
,射线![]() 为
为![]() 的“二倍角线”,则
的“二倍角线”,则![]() 的大小是______;
的大小是______;
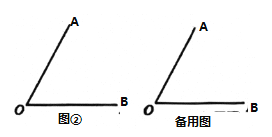
(解决问题)如图②,己知![]() ,射线
,射线![]() 从
从![]() 出发,以
出发,以![]() /秒的速度绕
/秒的速度绕![]() 点逆时针旋转;射线
点逆时针旋转;射线![]() 从
从![]() 出发,以
出发,以![]() /秒的速度绕
/秒的速度绕![]() 点顺时针旋转,射线
点顺时针旋转,射线![]() ,
,![]() 同时出发,当其中一条射线回到出发位置的时候,整个运动随之停止,设运动的时间为
同时出发,当其中一条射线回到出发位置的时候,整个运动随之停止,设运动的时间为![]() 秒.
秒.
(3)当射线![]() ,
,![]() 旋转到同一条直线上时,求
旋转到同一条直线上时,求![]() 的值;
的值;
(4)若![]() ,
,![]() ,
,![]() 三条射线中,一条射线恰好是以另外两条射线为边组成的角的“二倍角线”,直接写出
三条射线中,一条射线恰好是以另外两条射线为边组成的角的“二倍角线”,直接写出![]() 所有可能的值______.
所有可能的值______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com