
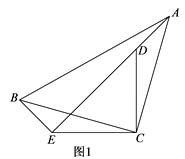
【题目】已知等腰RtABC与等腰RtCDE,∠ACB=∠DCE=90°.把RtABC绕点C旋转.
(1)如图1,当点A旋转到ED的延长线时,若![]() ,BE=5,求CD的长;
,BE=5,求CD的长;
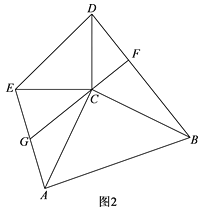
(2)当RtABC旋转到如图2所示的位置时,过点C作BD的垂线交BD于点F,交AE于点G,求证:BD=2CG.
【答案】(1)![]() ; (2)见解析.
; (2)见解析.
【解析】(1)根据旋转的性质,得到∠ADC=∠BEC=135°,进而得到∠AEB=90°,再根据勾股定理以及AD的长,即可得出DE=7,最后根据等腰Rt△CDE,运用勾股定理得到CD的长;
(2)过点A作AH∥CE,交CG的延长线于H,连接HE,则∠CAH+∠ACE=180°,再根据∠BCD+∠ACE=180°,即可得到∠CAE=∠BCD,再判定△BCD≌△CAH(ASA),得出AH=CD=CE,BD=CH,再判定四边形ACEH是平行四边形,即可得到CH=2CG,进而得出BD=2CG.
(1)如图1,
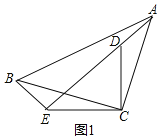
∵△ADC是由△BEC绕点C旋转得到的,
∴AD=BE=5,∠ADC=∠BEC,
∵在等腰Rt△ABC与等腰Rt△CDE中,BC=AC=![]() ,∠EDC=∠DEC=45°,
,∠EDC=∠DEC=45°,
∴AB=13,∠ADC=∠BEC=135°,
∴∠AEB=90°,
∴AE=![]() =12,
=12,
∴DE=7,
∴等腰Rt△CDE中,CD=![]() DE=
DE=![]() ;
;
(2)如图2,过点A作AH∥CE,交CG的延长线于H,连接HE,则∠CAH+∠ACE=180°,
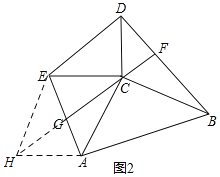
∵∠ACB=∠DCE=90°,
∴∠BCD+∠ACE=180°,
∴∠CAE=∠BCD,
∵CF⊥BD,∠ACB=90°,
∴∠CBF+∠BCF=∠ACG+∠BCF=90°,
∴∠CBF=∠ACG,
在△BCD和△CAH中,
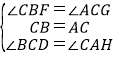 ,
,
∴△BCD≌△CAH(ASA),
∴AH=CD=CE,BD=CH,
又∵AH∥CE,
∴四边形ACEH是平行四边形,
∴CH=2CG,
∴BD=2CG.


科目:初中数学 来源: 题型:
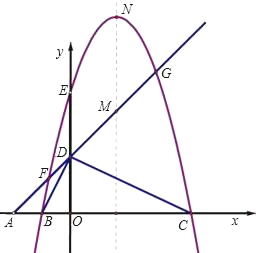
【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组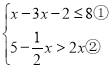 并求其整数解的和.
并求其整数解的和.
解:解不等式①,得_______;
解不等式②,得________;
把不等式①和②的解集在数轴上表示出来:
![]()
![]() 原不等式组的解集为________,
原不等式组的解集为________,
由数轴知其整数解为________,和为________.
在解答此题的过程中我们借助于数轴上,很直观地找出了原不等式组的解集及其整数解,这就是“数形结合的思想”,同学们要善于用数形结合的思想去解决问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,斜坡AB的坡度![]() ,仰角∠CBE=50°.则山峰的高度CF约为( )米.(可用的参考数据:sin50°≈0.8,tan50°≈1.2,
,仰角∠CBE=50°.则山峰的高度CF约为( )米.(可用的参考数据:sin50°≈0.8,tan50°≈1.2, ![]() )
)
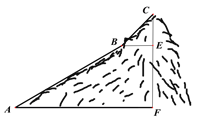
A. 500 B. 518 C. 530 D. 580
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委为积极参与“陶行知杯.全国书法大赛”现场决赛,向学校学生征集书画作品,今年3月份举行了“书画比赛”初赛,初赛成绩评定为A,B,C,D,E五个等级.该校七年级书法班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题.
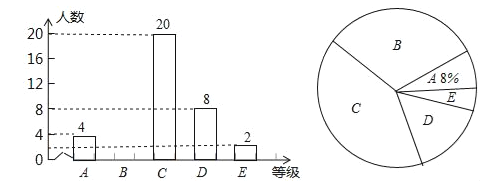
(1)该校七年级书法班共有 名学生;扇形统计图中C等级所对应扇形的圆心角等于 度,并补全条形统计图;
(2)A等级的4名学生中有2名男生,2名女生,现从中任意选取2名学生参加“陶行知杯.全国书法大赛”现场决赛,请你用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后超过部分按原价85折优惠设顾客预计累计购物![]() 元(
元(![]() )
)
(1)请用含![]() 的代数式分别表示顾客在两家超市购物所付的费用;
的代数式分别表示顾客在两家超市购物所付的费用;
(2)某顾客分别到两家超市买了相同的货物,并且所付费用也相同你知道这位顾客共花了多少钱吗?请列出方程解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC.
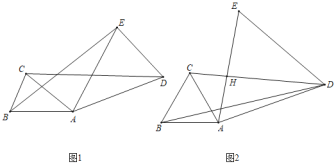
(1)如图1,在△ADE中,若AD=AE,且∠DAE=∠BAC,求证:CD=BE;
(2)如图2,在△ADE中,若∠DAE=∠BAC=60°,且CD垂直平分AE,AD=6,CD=8,求BD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了科学建设“学生健康成长工程”.随机抽取了部分学生家庭对其家长进行了主题为“周末孩子在家您关心吗?”的问卷调查,将回收的问卷进行分析整理,得到了如下的样本统计表和扇形统计图:
代号 | 情况分类 | 家庭数 |
| 带孩子玩并且关心其作业完成情况 | 16 |
| 只关心其作业完成情况 | b |
| 只带孩子玩 | 8 |
| 既不带孩子玩也不关心其作业完成情况 | d |
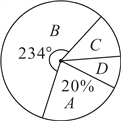
(1)求![]() 的值;
的值;
(2)该校学生家庭总数为500,学校决定按比例在![]() 类家庭中抽取家长组成培训班,其比例为
类家庭中抽取家长组成培训班,其比例为![]() 类取20%,
类取20%,![]() 类各取60%,请你估计该培训班的家庭数;
类各取60%,请你估计该培训班的家庭数;
(3)若在![]() 类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在
类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在![]() 类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.
类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com