
【题目】已知△ABC中,AB=AC.
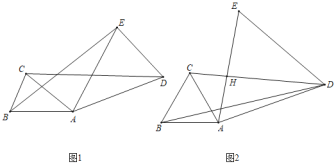
(1)如图1,在△ADE中,若AD=AE,且∠DAE=∠BAC,求证:CD=BE;
(2)如图2,在△ADE中,若∠DAE=∠BAC=60°,且CD垂直平分AE,AD=6,CD=8,求BD的长
【答案】(1)详见解析;(2)BD=10.
【解析】
(1)根据SAS证明△BAE和△CAD全等,再利用全等三角形的性质证明即可;
(2)根据等边三角形的性质和含30°的直角三角形的性质解答即可.
解:(1)∵∠DAE=∠BAC,
∴∠BAE=∠CAD,
在△BAE和△CAD中,
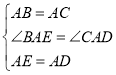 ,
,
∴△BAE≌△CAD(SAS),
∴CD=BE;
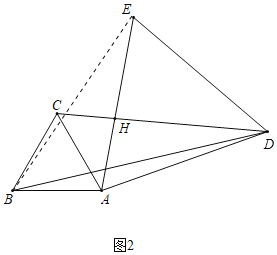
(2)解:连接BE,如图2所示:
∵AD=AE,∠DAE=60°,
∴△ADE是等边三角形,
∵CD垂直平分AE,
∴∠CDA=![]() ∠ADE=
∠ADE=![]() ×60°=30°,
×60°=30°,
∵△BAE≌△CAD,
∴BE=CD=8,∠BEA=∠CDA=30°,
∴BE⊥DE,
DE=AD=6,
∴BD=![]() =10.
=10.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
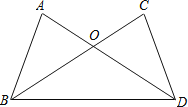
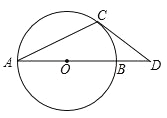
【题目】(1)如图,AD、BC相交于点O,OA=OC,∠OBD=∠ODB.求证:AB=CD.
(2)如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若OD=![]() ,求∠BAC的度数.
,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题:(假设行车过程没有停车等时,且平均车速为0.5千米/分钟)
华夏专车 | 神州专车 | |
里程费 | 1.8元/千米 | 2元/千米 |
时长费 | 0.3元/分钟 | 0.6元/分钟 |
远途费 | 0.8元/千米产(超过7千米部分) | 无 |
起步价 | 无 | 10元 |
华夏专车:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7千米以内(含7千米)不收远途费,超过7千米的,超出的部分按每千米加收0.8元. 神州专车:车费由里程费、时长费、起步价三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;起步价与行车距离无关. | ||
(1)小明在该地区出差,乘车距离为10千米,如果小明使用华夏专车,需要支付的打车费用为 元;
(2)小强在该地区从甲地乘坐神州专车到乙地,一共花费42元,求甲乙两地距离是多少千米?
(3)神州专车为了和华夏专车竞争客户,分别推出了优惠方式,华夏专车对于乘车路程在7千米以上(含7千米)的客户每次收费立减9元;神州打车车费5折优惠.对采用哪一种打车方式更合算提出你的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
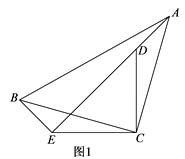
【题目】已知等腰RtABC与等腰RtCDE,∠ACB=∠DCE=90°.把RtABC绕点C旋转.
(1)如图1,当点A旋转到ED的延长线时,若![]() ,BE=5,求CD的长;
,BE=5,求CD的长;
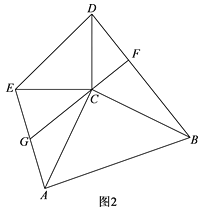
(2)当RtABC旋转到如图2所示的位置时,过点C作BD的垂线交BD于点F,交AE于点G,求证:BD=2CG.
查看答案和解析>>
科目:初中数学 来源: 题型:
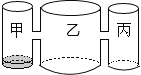
【题目】实验室里,水平圆桌面上有甲乙丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两根相同的管子在容器的5cm高度处连接(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位高度为![]() cm,则开始注入________分钟的水量后,甲与乙的水位高度之差是
cm,则开始注入________分钟的水量后,甲与乙的水位高度之差是![]() cm.
cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
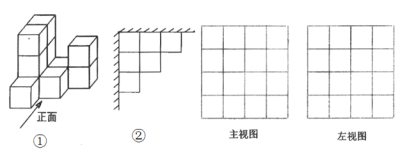
【题目】在平整的地面上,由若干个完全相同的棱长为10 cm的小正方体堆成一个几何体,如图①所示.
(1)请你在方格纸中分别画出这个几何体的主视图和左视图;
(2)若现在手头还有一些相同的小正方体,如果保持这个几何体的主视图和俯视图不变,
Ⅰ.在图①所示几何体上最多可以添加 个小正方体;
Ⅱ.在图①所示几何体上最多可以拿走 个小正方体;
Ⅲ.在题Ⅱ的情况下,把这个几何体放置在墙角,使得几何体的左面和后面靠墙,其俯视图如图②所示,若给该几何体露在外面的面喷上红漆,则需要喷漆的面积最少是多少平方厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
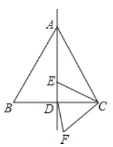
【题目】如图,边长为4的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF,则在点E运动过程中,DF的最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角三角板![]() 和直角三角板
和直角三角板![]() ,
,![]() ,
,![]() ,
,![]() .
.
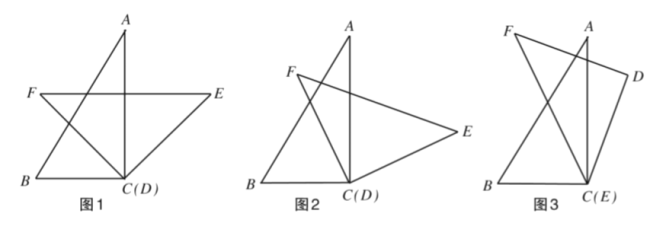
(1)如图1,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 平分
平分![]() 时,求
时,求![]() 的度数;
的度数;
(2)在(1)的条件下,继续旋转三角板![]() ,猜想
,猜想![]() 与
与![]() 有怎样的数量关系?并利用图2所给的情形说明理由;
有怎样的数量关系?并利用图2所给的情形说明理由;
(3)如图3,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转.当
旋转.当![]() 落在
落在![]() 内部时,直接写出
内部时,直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com