练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

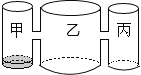
    【题目】实验室里，水平圆桌面上有甲乙丙三个圆柱形容器(容器足够高)，底面半径之比为1:2:1，用两根相同的管子在容器的5cm高度处连接(即管子底端离容器底5cm)，现三个容器中，只有甲中有水，水位高1cm，如图所示.若每分钟同时向乙和丙注入相同量的水，开始注水1分钟，乙的水位高度为cm，则开始注入________分钟的水量后，甲与乙的水位高度之差是cm.

    【答案】1,,.

    【解析】

    先根据题意算出乙和丙每分钟注水量,随着时间变化可以分三种情况讨论,①当甲比乙高,②乙比加高,③乙溢出到甲后,乙比甲高.

    试题∵甲、乙、丙三个圆柱形容器（容器足够高），底面半径之比为1:2:1，

    ∴甲、乙、丙三个圆柱形容器的底面积之比为1：4：1，

    ∵每分钟同时向乙和丙注入相同量的水，注水1分钟，乙的水位上升cm，

    ∴注水1分钟，丙的水位上升cm，

    ①当甲比乙高cm时，此时乙中水位高cm，用时1分；

    ②当乙比甲水位高cm 时,乙应为cm, 分,

    当丙的高度到5cm时，此时用时为5÷=分，

    因为,所以分乙比甲高cm.

    ③当丙高5cm时,此时乙中水高cm，在这之后丙中的水流入乙中，乙每分钟水位上升cm，当乙的水位达到5cm时开始流向甲，此时用时为=分，甲水位每分上升cm，当甲的水位高为cm时，乙比甲高cm，此时用时分；

    综上，开始注入1,,分钟的水量后，甲与乙的水位高度之差是cm.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

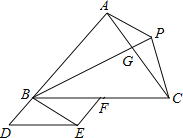
    【题目】如图，点D是△ABC的边AB的延长线上一点，点F是边BC上的一个动点（不与点B重合）．以BD、BF为邻边作平行四边形BDEF，又AP∥BE，AP＝BE，（点P、E在直线AB的同侧），如果BD＝AB，那么△PBC的面积与△ABC面积之比为（　　）.

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校新到一批理、化、生实验器材需要整理，若实验管理员李老师一人单独整理需要40分钟完成，现在李老师与工人王师傅共同整理20分钟后，李老师因事外出，王师傅再单独整理了20分钟才完成任务．

    （1）王师傅单独整理这批实验器材需要多少分钟？

    （2）学校要求王师傅的工作时间不能超过30分钟，要完成整理这批器材，李老师至少要工作多少分钟？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校团委为积极参与“陶行知杯．全国书法大赛”现场决赛，向学校学生征集书画作品，今年3月份举行了“书画比赛”初赛，初赛成绩评定为A，B，C，D，E五个等级．该校七年级书法班全体学生参加了学校的比赛，并将比赛结果绘制成如下两幅不完整的统计图．请根据图中信息，解答下列问题．

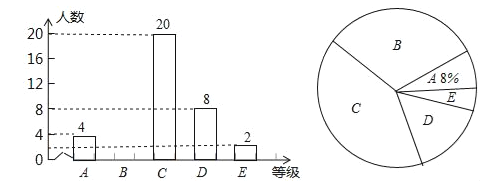
    （1）该校七年级书法班共有 名学生；扇形统计图中C等级所对应扇形的圆心角等于 度，并补全条形统计图；

    （2）A等级的4名学生中有2名男生，2名女生，现从中任意选取2名学生参加“陶行知杯．全国书法大赛”现场决赛，请你用列表法或画树状图的方法，求出恰好选到1名男生和1名女生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个形如的五位自然数（其中a表示该数的万位上的数字，b表示该数的千位上的数字，c表示该数的百位上的数字，d表示该数的十位上的数字，e表示该数的个位上的数字，且），若有且，则把该自然数叫做“对称数”，例如在自然数12321中，3=2+1，则12321是一个“对称数”. 同时规定：若该“对称数”的前两位数与后两位数的平方差被693的奇数倍，则称该“对称数”为“智慧对称数”.如在“对称数”43734中，，则43734是一个“智慧对称数”．

    （1）将一个“对称数”的个位上与十位上的数字交换位置，同时，将千位上与万位上的数字交换位置，称交换前后的这两个“对称数”为一组“相关对称数”。例如：12321与21312为一组“相关对称数”， 求证：任意的一组“相关对称数”之和是最小“对称数”的倍数；

    （2）求出所有的“智慧对称数”中的最大“智慧对称数”．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC中，AB＝AC．

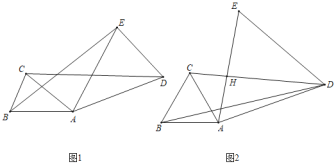
    （1）如图1，在△ADE中，若AD＝AE，且∠DAE＝∠BAC，求证：CD＝BE；

    （2）如图2，在△ADE中，若∠DAE＝∠BAC＝60°，且CD垂直平分AE，AD＝6，CD＝8，求BD的长

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】交通道路的不断完善，带动了旅游业的发展，某市旅游景区有A，B，C，D，E等著名景点，该市旅游部门统计绘制出2018年“五·一”小长假期间旅游情况统计图，根据图中信息回答下列问题：

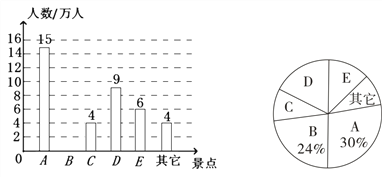
    （1）2018年“五·一”期间，该市景点共接待游客　 　万人，扇形统计图中C景点所对应的圆心角的度数是　 　，并补全条形统计图．

    （2）根据近几年到该市旅游人数增长趋势，预计2018年“十·一”国庆节将有80万游客选择该市旅游，E景点每张门票是25元，请估计2018年“十·一”国庆期间E景点门票收入约是多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数轴是初中数学的一个重要工具，利用数轴可以将数与形完美结合．研究数轴时，我们发现有许多重要的规律:例如，若数轴上点 A , B 表示的数分别为 a , b ，则 A , B 两点之间的距离AB=，线段 AB 的中点M 表示的数为．如图，在数轴上，点A,B,C表示的数分别为-8，2，20．

    （1）如果点A和点C都向点B运动，且都用了4秒钟，那么这两点的运动速度分别是点A每秒_______个单位长度、点C每秒______个单位长度；

    （2）如果点A以每秒1个单位长度沿数轴的正方向运动，点C以每秒3个单位长度沿数轴的负方向运动，设运动时间为t秒，请问当这两点与点B距离相等的时候，t为何值？

    （3）如果点A以每秒1个单位长度沿数轴的正方向运动，点B以每秒3个单位长度沿数轴的正方向运动，且当它们分别到达C点时就停止不动，设运动时间为t秒，线段AB的中点为点P；

    ①　t为何值时PC=12；

    ②　t为何值时PC=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我国古代数学著作《九章算术》中的一个问题．原文是：今有池方一丈，葭生其中央，出水尺．引葭赴岸，适与岸齐问水深、葭长各几何译文大意是：如图，有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺．如果把这根芦苇拉向水池边的中点，它的顶端恰好到达池边的水面．问水的深度与这根芦苇的长度分别是多少？

    查看答案和解析>>

    同步练习册答案