
ЁОЬтФПЁПЪ§жсЪЧГѕжаЪ§бЇЕФвЛИіживЊЙЄОпЃЌРћгУЪ§жсПЩвдНЋЪ§гыаЮЭъУРНсКЯЃЎбаОПЪ§жсЪБЃЌЮвУЧЗЂЯжгааэЖрживЊЕФЙцТЩ:Р§ШчЃЌШєЪ§жсЩЯЕу A , B БэЪОЕФЪ§ЗжБ№ЮЊ a , b ЃЌдђ A , B СНЕужЎМфЕФОрРыAB=![]() ЃЌЯпЖЮ AB ЕФжаЕуM БэЪОЕФЪ§ЮЊ
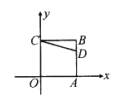
ЃЌЯпЖЮ AB ЕФжаЕуM БэЪОЕФЪ§ЮЊ![]() ЃЎШчЭМЃЌдкЪ§жсЩЯЃЌЕуA,B,CБэЪОЕФЪ§ЗжБ№ЮЊ-8ЃЌ2ЃЌ20ЃЎ
ЃЎШчЭМЃЌдкЪ§жсЩЯЃЌЕуA,B,CБэЪОЕФЪ§ЗжБ№ЮЊ-8ЃЌ2ЃЌ20ЃЎ

ЃЈ1ЃЉШчЙћЕуAКЭЕуCЖМЯђЕуBдЫЖЏЃЌЧвЖМгУСЫ4УыжгЃЌФЧУДетСНЕуЕФдЫЖЏЫйЖШЗжБ№ЪЧЕуAУПУы_______ИіЕЅЮЛГЄЖШЁЂЕуCУПУы______ИіЕЅЮЛГЄЖШЃЛ
ЃЈ2ЃЉШчЙћЕуAвдУПУы1ИіЕЅЮЛГЄЖШбиЪ§жсЕФе§ЗНЯђдЫЖЏЃЌЕуCвдУПУы3ИіЕЅЮЛГЄЖШбиЪ§жсЕФИКЗНЯђдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЌЧыЮЪЕБетСНЕугыЕуBОрРыЯрЕШЕФЪБКђЃЌtЮЊКЮжЕЃП
ЃЈ3ЃЉШчЙћЕуAвдУПУы1ИіЕЅЮЛГЄЖШбиЪ§жсЕФе§ЗНЯђдЫЖЏЃЌЕуBвдУПУы3ИіЕЅЮЛГЄЖШбиЪ§жсЕФе§ЗНЯђдЫЖЏЃЌЧвЕБЫќУЧЗжБ№ЕНДяCЕуЪБОЭЭЃжЙВЛЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЌЯпЖЮABЕФжаЕуЮЊЕуPЃЛ
ЂйЁЁtЮЊКЮжЕЪБPC=12ЃЛ
ЂкЁЁtЮЊКЮжЕЪБPC=4ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2.5ЃЛ4.5ЃЛЃЈ2ЃЉtЃН4Лђ7ЃЛЃЈ3ЃЉЂй![]() ЃЛЂк20
ЃЛЂк20
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЪ§жсЩЯСНЕужЎМфЕФОрРыЙЋЪНЧѓГіABЕФГЄКЭBCЕФГЄЃЌШЛКѓИљОнЫйЖШ=ТЗГЬЁТЪБМфМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЗжЕуAКЭЕуCЯргіЧАAB=BCЁЂЯргіЪБAB=BCКЭЯргіКѓAB=BCШ§жжЧщПіЃЌЗжБ№ЛГіЖдгІЕФЭМаЮЃЌШЛКѓИљОнAB=BCСаГіЗНГЬЧѓГіtЕФМДПЩЃЛ
ЃЈ3ЃЉЂйЗжЕуBЕНДяЕуCжЎЧАКЭЕуBЕНДяЕуCжЎКѓЧвЕуAЕНЕуCжЎЧАСНжжЧщПіЃЌЗжБ№ЛГіЖдгІЕФЭМаЮЃЌРћгУжаЕуЙЋЪНЁЂСНЕужЎМфЕФОрРыЙЋЪНКЭPC=12СаЗНГЬМДПЩЧѓГіtЕФжЕЃЛ
ЂкЗжЕуBЕНДяЕуCжЎЧАКЭЕуBЕНДяЕуCжЎКѓЧвЕуAЕНЕуCжЎЧАСНжжЧщПіЃЌЗжБ№ЛГіЖдгІЕФЭМаЮЃЌРћгУжаЕуЙЋЪНЁЂСНЕужЎМфЕФОрРыЙЋЪНКЭPC=12СаЗНГЬМДПЩЧѓГіtЕФжЕЃЛ
НтЃКЃЈ1ЃЉЁпЕуA,B,CБэЪОЕФЪ§ЗжБ№ЮЊ-8ЃЌ2ЃЌ20ЃЎ
ЁрAB=2ЃЃЈ-8ЃЉ=10ЃЌBC=20Ѓ2=18
ЁпЕуAКЭЕуCЖМЯђЕуBдЫЖЏЃЌЧвЖМгУСЫ4УыжгЃЌ
ЁрЕуAЕФЫйЖШЮЊУПУыЃКABЁТ4=![]() ИіЕЅЮЛГЄЖШЃЌЕуCЕФЫйЖШЮЊУПУыЃКBCЁТ4=
ИіЕЅЮЛГЄЖШЃЌЕуCЕФЫйЖШЮЊУПУыЃКBCЁТ4=![]() ИіЕЅЮЛГЄЖШЃЌ
ИіЕЅЮЛГЄЖШЃЌ
ЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉAC=20ЃЃЈ-8ЃЉ=28
ЁрЕуAКЭЕуCЯргіЪБМфЮЊACЁТЃЈ1ЃЋ3ЃЉ=7s
ЕБЕуAКЭЕуCЯргіЧАЃЌAB=BCЪБЃЌДЫЪБ0ЃМtЃМ7ЃЌШчЯТЭМЫљЪО

ДЫЪБЕуAдЫЖЏЕФТЗГЬЮЊ1ЁСt=tЃЌЕуCдЫЖЏЕФТЗГЬЮЊ3ЁСt=3t
ЁрДЫЪБAB=10ЃtЃЌBC=18Ѓ3t
ЁпAB=BC
Ёр10Ѓt=18Ѓ3t
НтЕУЃКt=4ЃЛ
ЕБЕуAКЭЕуCЯргіЪБЃЌДЫЪБt=7ЃЌШчЯТЭМЫљЪО

ДЫЪБЕуAКЭЕуCжиКЯ
ЁрAB=BC
МДt=7ЃЛ
ЕБЕуAКЭЕуCЯргіКѓЃЌДЫЪБtЃО7ЃЌШчЯТЭМЫљЪО

гЩЕуCЕФЫйЖШДѓгкЕуAЕФЫйЖШ
ЁрДЫЪБBCЃОAB
ЙЪДЫЪБВЛДцдкtЃЌЪЙAB=BCЃЎ
злЩЯЫљЪіЃКЕБAЁЂCСНЕугыЕуBОрРыЯрЕШЕФЪБКђЃЌtЃН4Лђ7ЃЎ
ЃЈ3ЃЉЕуBЕНДяЕуCЕФЪБМфЮЊЃКBCЁТ3=6sЃЌЕуAЕНДяЕуCЕФЪБМфЮЊЃКACЁТ1=28s
ЂйЕБЕуBЕНДяЕуCжЎЧАЃЌМД0ЃМtЃМ6ЪБЃЌШчЯТЭМЫљЪО

ДЫЪБЕуAЫљБэЪОЕФЪ§ЮЊ-8ЃЋtЃЌЕуBЫљБэЪОЕФЪ§ЮЊ2ЃЋ3t
ЁрЯпЖЮABЕФжаЕуPБэЪОЕФЪ§ЮЊ![]()
ЁрPC=20ЃЃЈ2tЃ3ЃЉ=12
НтЕУЃКt=![]() ЃЛ
ЃЛ
ЕБЕуBЕНДяЕуCжЎКѓЧвЕуAЕНЕуCжЎЧАЃЌМД6ЁмtЃМ28ЪБЃЌШчЯТЭМЫљЪО

ДЫЪБЕуAЫљБэЪОЕФЪ§ЮЊ-8ЃЋtЃЌЕуBЫљБэЪОЕФЪ§ЮЊ20
ЁрЯпЖЮABЕФжаЕуPБэЪОЕФЪ§ЮЊ![]()
ЁрPC=20ЃЃЈ![]() ЃЉ=12
ЃЉ=12
НтЕУЃКt=4ЃЌВЛЗћКЯЧАЬсЬѕМўЃЌЙЪЩсШЅЃЎ
злЩЯЫљЪіЃКt=![]() ЪБЃЌPC=12ЃЛ
ЪБЃЌPC=12ЃЛ
ЂкЕБЕуBЕНДяЕуCжЎЧАЃЌМД0ЃМtЃМ6ЪБЃЌШчЯТЭМЫљЪО

ДЫЪБЕуAЫљБэЪОЕФЪ§ЮЊ-8ЃЋtЃЌЕуBЫљБэЪОЕФЪ§ЮЊ2ЃЋ3t
ЁрЯпЖЮABЕФжаЕуPБэЪОЕФЪ§ЮЊ![]()
ЁрPC=20ЃЃЈ2tЃ3ЃЉ=4
НтЕУЃКt=![]() ЃЌВЛЗћКЯЧАЬсЬѕМўЃЌЙЪЩсШЅЃЛ
ЃЌВЛЗћКЯЧАЬсЬѕМўЃЌЙЪЩсШЅЃЛ
ЕБЕуBЕНДяЕуCжЎКѓЧвЕуAЕНЕуCжЎЧАЃЌМД6ЁмtЃМ28ЪБЃЌШчЯТЭМЫљЪО

ДЫЪБЕуAЫљБэЪОЕФЪ§ЮЊ-8ЃЋtЃЌЕуBЫљБэЪОЕФЪ§ЮЊ20
ЁрЯпЖЮABЕФжаЕуPБэЪОЕФЪ§ЮЊ![]()
ЁрPC=20ЃЃЈ![]() ЃЉ=4
ЃЉ=4
НтЕУЃКt=20ЃЎ
злЩЯЫљЪіЃКЕБt=20ЪБЃЌPC=4ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮ![]() ЕФСНБп
ЕФСНБп![]() ЁЂ
ЁЂ![]() ЗжБ№дк
ЗжБ№дк![]() жсЁЂ
жсЁЂ![]() жсЩЯЃЌЕу
жсЩЯЃЌЕу![]() дкБп
дкБп![]() ЩЯЃЌвд
ЩЯЃЌвд![]() ЮЊжааФЃЌАб
ЮЊжааФЃЌАб![]() а§зЊ
а§зЊ![]() ЃЌдђа§зЊКѓЕу
ЃЌдђа§зЊКѓЕу![]() ЕФЖдгІЕу
ЕФЖдгІЕу![]() ЕФзјБъЪЧ________.
ЕФзјБъЪЧ________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
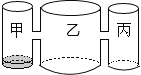
ЁОЬтФПЁПЪЕбщЪвРяЃЌЫЎЦНдВзРУцЩЯгаМзввБћШ§ИідВжљаЮШнЦї(ШнЦїзуЙЛИп)ЃЌЕзУцАыОЖжЎБШЮЊ1:2:1ЃЌгУСНИљЯрЭЌЕФЙмзгдкШнЦїЕФ5cmИпЖШДІСЌНг(МДЙмзгЕзЖЫРыШнЦїЕз5cm)ЃЌЯжШ§ИіШнЦїжаЃЌжЛгаМзжагаЫЎЃЌЫЎЮЛИп1cmЃЌШчЭМЫљЪО.ШєУПЗжжгЭЌЪБЯђввКЭБћзЂШыЯрЭЌСПЕФЫЎЃЌПЊЪМзЂЫЎ1ЗжжгЃЌввЕФЫЎЮЛИпЖШЮЊ![]() cmЃЌдђПЊЪМзЂШы________ЗжжгЕФЫЎСПКѓЃЌМзгыввЕФЫЎЮЛИпЖШжЎВюЪЧ
cmЃЌдђПЊЪМзЂШы________ЗжжгЕФЫЎСПКѓЃЌМзгыввЕФЫЎЮЛИпЖШжЎВюЪЧ![]() cm.
cm.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНећЕФЕиУцЩЯЃЌгЩШєИЩИіЭъШЋЯрЭЌЕФРтГЄЮЊ10 cmЕФаЁе§ЗНЬхЖбГЩвЛИіМИКЮЬхЃЌШчЭМЂйЫљЪО.
(1)ЧыФудкЗНИёжНжаЗжБ№ЛГіетИіМИКЮЬхЕФжїЪгЭМКЭзѓЪгЭМ;
(2)ШєЯждкЪжЭЗЛЙгавЛаЉЯрЭЌЕФаЁе§ЗНЬхЃЌШчЙћБЃГжетИіМИКЮЬхЕФжїЪгЭМКЭИЉЪгЭМВЛБфЃЌ
Ђё.дкЭМЂйЫљЪОМИКЮЬхЩЯзюЖрПЩвдЬэМг ИіаЁе§ЗНЬх;
Ђђ.дкЭМЂйЫљЪОМИКЮЬхЩЯзюЖрПЩвдФУзп ИіаЁе§ЗНЬх;
Ђѓ.дкЬтЂђЕФЧщПіЯТЃЌАбетИіМИКЮЬхЗХжУдкЧННЧЃЌЪЙЕУМИКЮЬхЕФзѓУцКЭКѓУцППЧНЃЌЦфИЉЪгЭМШчЭМЂкЫљЪОЃЌШєИјИУМИКЮЬхТЖдкЭтУцЕФУцХчЩЯКьЦсЃЌдђашвЊХчЦсЕФУцЛ§зюЩйЪЧЖрЩйЦНЗНРхУз?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊИпЬњЕФЫйЖШБШЖЏГЕЕФЫйЖШПь50 km/hЃЌаЁТЗЭЌбЇДгЫежнШЅББОЉгЮЭцЃЌБОДђЫуГЫзјЖЏГЕЃЌашвЊ6hВХФмЕНДяЃЛгЩгкЕУжЊПЊЭЈСЫИпЬњЃЌОіЖЈГЫзјИпЬњЃЌЫ§ЗЂЯжГЫзјИпЬњБШГЫзјЖЏГЕНкдМ72 minЃЎЧѓИпЬњЕФЫйЖШКЭЫежнгыББОЉжЎМфЕФОрРыЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
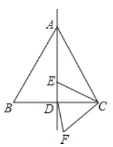
ЁОЬтФПЁПШчЭМЃЌБпГЄЮЊ4ЕФЕШБпШ§НЧаЮABCжаЃЌEЪЧЖдГЦжсADЩЯЕФвЛИіЖЏЕуЃЌСЌНгECЃЌНЋЯпЖЮECШЦЕуCФцЪБеыа§зЊ60ЁуЕУЕНFCЃЌСЌНгDFЃЌдђдкЕуEдЫЖЏЙ§ГЬжаЃЌDFЕФзюаЁжЕЪЧ______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЃН16ЃЌOЮЊABжаЕуЃЌЕуCдкЯпЖЮOBЩЯЃЈВЛгыЕуOЃЌBжиКЯЃЉЃЌНЋOCШЦЕуOФцЪБеыа§зЊ270ЁуКѓЕУЕНЩШаЮCODЃЌAPЃЌBQЗжБ№ЧагХЛЁ![]() гкЕуPЃЌQЃЌЧвЕуPЃЌ QдкABвьВрЃЌСЌНгOPЃЎ
гкЕуPЃЌQЃЌЧвЕуPЃЌ QдкABвьВрЃЌСЌНгOPЃЎ
ЃЈ1ЃЉЧѓжЄЃКAPЃНBQЃЛ
ЃЈ2ЃЉЕБBQЃН4![]() ЪБЃЌЧѓЩШаЮCOQЕФУцЛ§МА
ЪБЃЌЧѓЩШаЮCOQЕФУцЛ§МА![]() ЕФГЄЃЈНсЙћБЃСєІаЃЉЃЛ
ЕФГЄЃЈНсЙћБЃСєІаЃЉЃЛ
ЃЈ3ЃЉШєЁїAPOЕФЭтаФдкЩШаЮCODЕФФкВПЃЌЧыжБНгаДГіOCЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧѓВЛЕШЪНЃЈ2xЉ1ЃЉЃЈx+3ЃЉЃО0ЕФНтМЏЃЎ
НтЃКИљОнЁАЭЌКХСНЪ§ЯрГЫЃЌЛ§ЮЊе§ЁБПЩЕУЃКЂй![]() Лђ Ђк
Лђ Ђк![]() ЃЎ
ЃЎ
НтЂйЕУxЃО![]() ЃЛНтЂкЕУxЃМЉ3ЃЎ
ЃЛНтЂкЕУxЃМЉ3ЃЎ
ЁрВЛЕШЪНЕФНтМЏЮЊxЃО![]() ЛђxЃМЉ3ЃЎ
ЛђxЃМЉ3ЃЎ
ЧыФуЗТееЩЯЪіЗНЗЈНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓВЛЕШЪНЃЈ2xЉ3ЃЉЃЈx+1ЃЉЃМ0ЕФНтМЏЃЎ
ЃЈ2ЃЉЧѓВЛЕШЪН![]() Ён0ЕФНтМЏЃЎ
Ён0ЕФНтМЏЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГХЉПЦЫљЖдМзЁЂввСНжжаЁТѓИїбЁгУ10ПщУцЛ§ЯрЭЌЕФЪдбщЬяНјаажжжВЪдбщЃЌЫќУЧЕФЦНОљФЖВњСПЗжБ№ЪЧ![]() =610ЧЇПЫЃЌ
=610ЧЇПЫЃЌ![]() =608ЧЇПЫЃЌФЖВњСПЕФЗНВюЗжБ№ЪЧ
=608ЧЇПЫЃЌФЖВњСПЕФЗНВюЗжБ№ЪЧ![]() ="29." 6ЃЌ
="29." 6ЃЌ![]() ="2." 7. дђЙигкСНжжаЁТѓЭЦЙужжжВЕФКЯРэОіВпЪЧ ЃЈ ЃЉ
="2." 7. дђЙигкСНжжаЁТѓЭЦЙужжжВЕФКЯРэОіВпЪЧ ЃЈ ЃЉ
A. МзЕФЦНОљФЖВњСПНЯИпЃЌгІЭЦЙуМз
B. МзЁЂввЕФЦНОљФЖВњСПЯрВюВЛЖрЃЌОљПЩЭЦЙу
C. МзЕФЦНОљФЖВњСПНЯИпЃЌЧвФЖВњСПБШНЯЮШЖЈЃЌгІЭЦЙуМз
D. МзЁЂввЕФЦНОљФЖВњСПЯрВюВЛЖрЃЌЕЋввЕФФЖВњСПБШНЯЮШЖЈЃЌгІЭЦЙувв
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com