
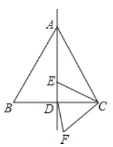
【题目】如图,边长为4的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF,则在点E运动过程中,DF的最小值是______.
【答案】1
【解析】
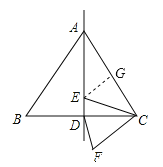
取AC的中点G,连接EG,根据等边三角形的性质可得CD=CG,再求出∠DCF=∠GCE,根据旋转的性质可得CE=CF,然后利用“边角边”证明△DCF和△GCE全等,再根据全等三角形对应边相等可得DF=EG,然后根据垂线段最短可得EG⊥AD时最短,再根据∠CAD=30°求解即可.
解:如图,取AC的中点G,连接EG,
∵旋转角为60°,
∴∠ECD+∠DCF=60°,
又∵∠ECD+∠GCE=∠ACB=60°,
∴∠DCF=∠GCE,
∵AD是等边△ABC的对称轴,
![]() ,
,
∴CD=CG,
又∵CE旋转到CF,
∴CE=CF,
在△DCF和△GCE中,
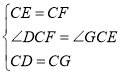 ,
,
∴△DCF≌△GCE(SAS),
∴DF=EG,
根据垂线段最短,EG⊥AD时,EG最短,即DF最短,
此时![]() ,
,![]() ,
,
![]()
∴DF=1.
故答案为:1.


科目:初中数学 来源: 题型:
【题目】解不等式组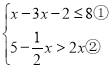 并求其整数解的和.
并求其整数解的和.
解:解不等式①,得_______;
解不等式②,得________;
把不等式①和②的解集在数轴上表示出来:
![]()
![]() 原不等式组的解集为________,
原不等式组的解集为________,
由数轴知其整数解为________,和为________.
在解答此题的过程中我们借助于数轴上,很直观地找出了原不等式组的解集及其整数解,这就是“数形结合的思想”,同学们要善于用数形结合的思想去解决问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC.
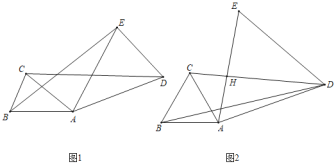
(1)如图1,在△ADE中,若AD=AE,且∠DAE=∠BAC,求证:CD=BE;
(2)如图2,在△ADE中,若∠DAE=∠BAC=60°,且CD垂直平分AE,AD=6,CD=8,求BD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了科学建设“学生健康成长工程”.随机抽取了部分学生家庭对其家长进行了主题为“周末孩子在家您关心吗?”的问卷调查,将回收的问卷进行分析整理,得到了如下的样本统计表和扇形统计图:
代号 | 情况分类 | 家庭数 |
| 带孩子玩并且关心其作业完成情况 | 16 |
| 只关心其作业完成情况 | b |
| 只带孩子玩 | 8 |
| 既不带孩子玩也不关心其作业完成情况 | d |
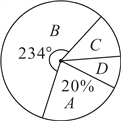
(1)求![]() 的值;
的值;
(2)该校学生家庭总数为500,学校决定按比例在![]() 类家庭中抽取家长组成培训班,其比例为
类家庭中抽取家长组成培训班,其比例为![]() 类取20%,
类取20%,![]() 类各取60%,请你估计该培训班的家庭数;
类各取60%,请你估计该培训班的家庭数;
(3)若在![]() 类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在
类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在![]() 类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.
类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美结合.研究数轴时,我们发现有许多重要的规律:例如,若数轴上点 A , B 表示的数分别为 a , b ,则 A , B 两点之间的距离AB=![]() ,线段 AB 的中点M 表示的数为
,线段 AB 的中点M 表示的数为![]() .如图,在数轴上,点A,B,C表示的数分别为-8,2,20.
.如图,在数轴上,点A,B,C表示的数分别为-8,2,20.

(1)如果点A和点C都向点B运动,且都用了4秒钟,那么这两点的运动速度分别是点A每秒_______个单位长度、点C每秒______个单位长度;
(2)如果点A以每秒1个单位长度沿数轴的正方向运动,点C以每秒3个单位长度沿数轴的负方向运动,设运动时间为t秒,请问当这两点与点B距离相等的时候,t为何值?
(3)如果点A以每秒1个单位长度沿数轴的正方向运动,点B以每秒3个单位长度沿数轴的正方向运动,且当它们分别到达C点时就停止不动,设运动时间为t秒,线段AB的中点为点P;
① t为何值时PC=12;
② t为何值时PC=4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,老师在屏幕上出示了一个例题:在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,画出图形(如图),给出下列四个条件:①∠DBO=∠ECO;②∠BDO=∠CEO;③BD=CE;④OB=OC.
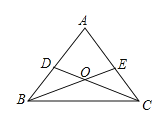
(1)要求同学从这四个等式中选出两个作为已知条件,可判定△ABC是等腰三角形.
请你用序号在横线上写出所有情形.答:
(2)选择第(1)题中的一种情形,说明△ABC是等腰三角形的理由,并写出解题过程.
解:我选择 .
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的顶点
的顶点![]() 在第一象限,点
在第一象限,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,![]() ,
,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() 与
与![]() 关于点
关于点![]() 成中心对称,则点
成中心对称,则点![]() 的坐标为( )
的坐标为( )
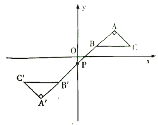
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
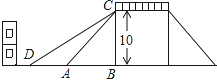
【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=![]() :3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com