
【题目】某中学为了科学建设“学生健康成长工程”.随机抽取了部分学生家庭对其家长进行了主题为“周末孩子在家您关心吗?”的问卷调查,将回收的问卷进行分析整理,得到了如下的样本统计表和扇形统计图:
代号 | 情况分类 | 家庭数 |
| 带孩子玩并且关心其作业完成情况 | 16 |
| 只关心其作业完成情况 | b |
| 只带孩子玩 | 8 |
| 既不带孩子玩也不关心其作业完成情况 | d |
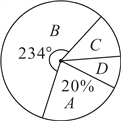
(1)求![]() 的值;
的值;
(2)该校学生家庭总数为500,学校决定按比例在![]() 类家庭中抽取家长组成培训班,其比例为
类家庭中抽取家长组成培训班,其比例为![]() 类取20%,
类取20%,![]() 类各取60%,请你估计该培训班的家庭数;
类各取60%,请你估计该培训班的家庭数;
(3)若在![]() 类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在
类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在![]() 类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.
类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD是一块绿化带,阴影部分EOFB,GHMN都是正方形的花圃,其中EOFB的顶点O是正方形中心.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰RtABC与等腰RtCDE,∠ACB=∠DCE=90°.把RtABC绕点C旋转.
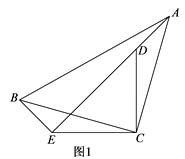
(1)如图1,当点A旋转到ED的延长线时,若![]() ,BE=5,求CD的长;
,BE=5,求CD的长;
(2)当RtABC旋转到如图2所示的位置时,过点C作BD的垂线交BD于点F,交AE于点G,求证:BD=2CG.
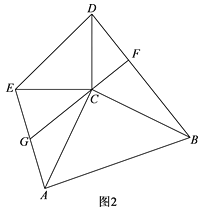
查看答案和解析>>
科目:初中数学 来源: 题型:
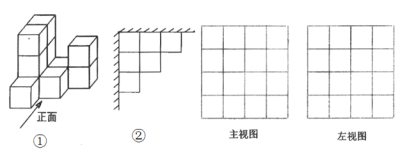
【题目】在平整的地面上,由若干个完全相同的棱长为10 cm的小正方体堆成一个几何体,如图①所示.
(1)请你在方格纸中分别画出这个几何体的主视图和左视图;
(2)若现在手头还有一些相同的小正方体,如果保持这个几何体的主视图和俯视图不变,
Ⅰ.在图①所示几何体上最多可以添加 个小正方体;
Ⅱ.在图①所示几何体上最多可以拿走 个小正方体;
Ⅲ.在题Ⅱ的情况下,把这个几何体放置在墙角,使得几何体的左面和后面靠墙,其俯视图如图②所示,若给该几何体露在外面的面喷上红漆,则需要喷漆的面积最少是多少平方厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,正方形![]() 的边长为
的边长为![]() ,动点
,动点![]() 从点
从点![]() 出发,在正方形的边上沿
出发,在正方形的边上沿![]() 运动,设运动的时间为
运动,设运动的时间为![]() ,点
,点![]() 移动的路程为
移动的路程为![]() ,
,![]() 与
与![]() 的函数图象如图②,请回答下列问题:
的函数图象如图②,请回答下列问题:

(1)点![]() 在
在![]() 上运动的时间为
上运动的时间为 ![]() ,在
,在![]() 上运动的速度为
上运动的速度为 ![]()
(2)设![]() 的面积为
的面积为![]() ,求当点
,求当点![]() 在
在![]() 上运动时,
上运动时,![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
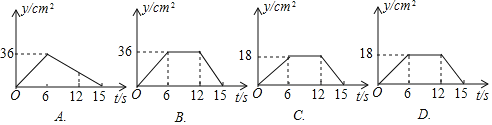
(3)①下列图表示![]() 的面积
的面积![]() 与时间
与时间![]() 之间的函数图象是 .
之间的函数图象是 .
②当![]()
![]() 时,
时,![]() 的面积为
的面积为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
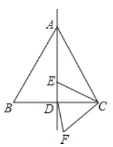
【题目】如图,边长为4的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF,则在点E运动过程中,DF的最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
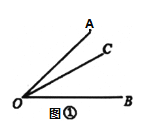
【题目】(理解新知)如图①,已知![]() ,在
,在![]() 内部画射线
内部画射线![]() ,得到三个角,分别为
,得到三个角,分别为![]() ,
,![]() ,
,![]() ,若这三个角中有一个角是另外一个角的两倍,则称射线
,若这三个角中有一个角是另外一个角的两倍,则称射线![]() 为
为![]() 的“二倍角线”.
的“二倍角线”.
(1)一个角的角平分线______这个角的“二倍角线”(填“是”或“不是”)
(2)若![]() ,射线
,射线![]() 为
为![]() 的“二倍角线”,则
的“二倍角线”,则![]() 的大小是______;
的大小是______;
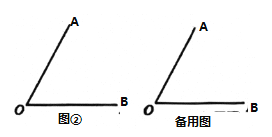
(解决问题)如图②,己知![]() ,射线
,射线![]() 从
从![]() 出发,以
出发,以![]() /秒的速度绕
/秒的速度绕![]() 点逆时针旋转;射线
点逆时针旋转;射线![]() 从
从![]() 出发,以
出发,以![]() /秒的速度绕
/秒的速度绕![]() 点顺时针旋转,射线
点顺时针旋转,射线![]() ,
,![]() 同时出发,当其中一条射线回到出发位置的时候,整个运动随之停止,设运动的时间为
同时出发,当其中一条射线回到出发位置的时候,整个运动随之停止,设运动的时间为![]() 秒.
秒.
(3)当射线![]() ,
,![]() 旋转到同一条直线上时,求
旋转到同一条直线上时,求![]() 的值;
的值;
(4)若![]() ,
,![]() ,
,![]() 三条射线中,一条射线恰好是以另外两条射线为边组成的角的“二倍角线”,直接写出
三条射线中,一条射线恰好是以另外两条射线为边组成的角的“二倍角线”,直接写出![]() 所有可能的值______.
所有可能的值______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“城有二姝,小艺与迎迎.小艺行八十步,迎迎行六十.今迎迎先行百步,小艺追之,问几何步及之?(改编自《九章算术》)”(步:古长度单位,1步约合今1.5米.)大意:在相同的时间里,小艺走80步,迎迎可走60步.现让迎迎先走100步,小艺开始追迎迎,问小艺需走多少步方可追上迎迎?
(1)在相同的时间里:
①若小艺走160步,则迎迎可走________步;
②若小艺走![]() 步,则迎迎可走_________步;
步,则迎迎可走_________步;
(2)求小艺追上迎迎时所走的步数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com